Question

【题目】如图，抛物线与轴交于、两点，与轴交于点,抛物线的对称轴为直线，交抛物线于点,交轴于点．

　　　　　　　　

（1）求抛物线的函数表达式及点、点的坐标；

（2）抛物线对称轴上的一动点从点出发，以每秒1个单位的速度向上运动，连接，，设运动时间为秒（），在点的运动过程中，请求出：当为何值时，？

（3）若点在抛物线上、两点之间运动（点不与点、重合），在运动过程中，设点的横坐标为，的面积为，求关于的函数关系式，并求为何值时有最大值，最大值是多少？

Answer 1

【答案】（1），，；（2）=；（3），当为时有最大值，最大值是．

【解析】

（1）根据对称轴和A点坐标可确定B点坐标，然后将A、B坐标代入抛物线求出a，b的值，即可得到解析式，然后将代入解析式，即可求出D坐标；

（2）秒时，点，先利用两点间的距离公式表示出，，，再根据勾股定理建立方程求解；

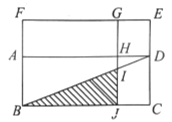
（3）作直线轴于点，交于，首先求直线BC解析式，用t表示出Q和G的坐标，得出QG的长度，然后利用三角形面积公式得到S与t的函数关系式，再根据二次函数的性质求最值即可．

（1）∵抛物线与轴交于，抛物线的对称轴为直线，

∴点.

将，代入抛物线中，

得，解得

抛物线的表达式为：

抛物线的对称轴为，

当时，

∴点.

（2）如图，

秒时，点，

，，

∵

∴，

即，整理得

解得：（舍去）

所以当=时，；

（3）如图，作直线轴于点，交于.

将代入，得

点的坐标为，

设直线的函数表达式为，

由两点的坐标得，解得

直线的函数表达式为,

点的横坐标为，

点的坐标为，点的坐标为

点的坐标为

∵，

有最大值，当时，最大

综上，与的函数表达式为，当为时有最大值，最大值是.