题目内容
1．（1）分解因式：3a（x2+4）2-48ax2（2）已知x+$\frac{1}{x}$=3，求（x-$\frac{1}{x}$）2的值．
分析 （1）首先提取公因式3a，进而利用平方差和完全平方公式分解因式得出即可；
（2）首先利用已知结合完全平方公式化简求出即可．
解答 解：（1）3a（x2+4）2-48ax2
=3a[（x2+4）2-16x2]
=3a（x2+4+4x）（x2+4-4x）
=3a（x+2）2（x-2）2；
（2）∵x+$\frac{1}{x}$=3，
∴（x+$\frac{1}{x}$）2=9，
则x2+$\frac{1}{{x}^{2}}$+2=9，
即x2+$\frac{1}{{x}^{2}}$=7，
∴（x-$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$-2=7-2=5．
点评 此题主要考查了提取公因式法以及公式法分解因式和完全平方公式的应用，正确应用乘法公式是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
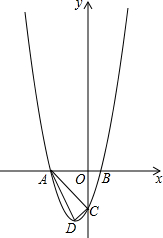如图，抛物线y=x2+bx+c的顶点为D（-1，-4），与y轴交于点C（0，-3），与x轴交于A，B两点（点A在点B的左侧）．