题目内容
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形,如果能,请求出点 H的坐标;如果不能,请说明理由.
H的坐标;如果不能,请说明理由.
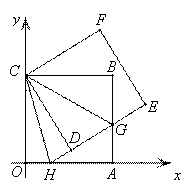
(1)略
(2)∠HCG=45° HG=OH+BG 理由略
(3)当G为AB的中点时,四边形AEBD可为矩形.此时H(2,0),过程略.

练习册系列答案
相关题目
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
| 摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当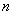 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率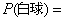 .
.
(3)试估算盒子里黑、白两种颜色的球各有多少只?
 的值为整数,则整数
的值为整数,则整数 =_____.
=_____. △ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,
△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC, ,则
,则 的值等于_______.
的值等于_______.

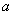 ,1×
,1×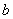 ,
,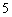 后的面积可以得到一个等式,这个等式是__________________________。
后的面积可以得到一个等式,这个等式是__________________________。
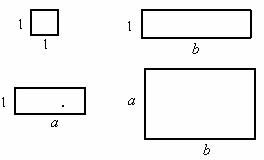
 究】对于一个正整数n,若能找到正整数
究】对于一个正整数n,若能找到正整数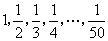 共50个数字。李老师要求同学们进行以下操作:每次操作先从黑板上的数中任选取2个数
共50个数字。李老师要求同学们进行以下操作:每次操作先从黑板上的数中任选取2个数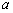 、
、
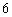 下的数.
下的数. 中,
中, ,∠
,∠ ,
, 的垂直平分线
的垂直平分线 交
交 于
于 ,交
,交 ,下列结论错误的是( )
,下列结论错误的是( ) 平分∠
平分∠
 B.△
B.△ 的周长等于
的周长等于
 D.点
D.点 是线段
是线段