题目内容
3.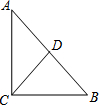 如图,△ABC中,∠ACB=90°,D为AB中点,BC=6,CD=5,则AB=10,AC=8.
如图,△ABC中,∠ACB=90°,D为AB中点,BC=6,CD=5,则AB=10,AC=8.
分析 由直角三角形斜边上的中线性质得出AB=2CD=10,再由勾股定理求出AC即可.
解答 解:∵∠ACB=90°,D为AB中点,
∴AB=2CD=10,
由勾股定理得:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8;
故答案为:10,8.
点评 本题考查了勾股定理、直角三角形斜边上的中线性质;熟练掌握勾股定理,由直角三角形斜边上的中线性质求出AB是解决问题的关键.

练习册系列答案
相关题目
11.分式$\frac{x}{4a}$,$\frac{x-y}{{x}^{2}-{y}^{2}}$,$\frac{a+b}{a-b}$,$\frac{(x+y)^{2}}{xy+{y}^{2}}$,$\frac{4}{2x-6}$中,最简分式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{2x-y=7}\\{3y=2x-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{xy=12}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{y}{3}-\frac{x}{2}-1}\\{2{x}^{2}+3y-15}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{x}-\frac{2}{y}=1}\\{x+y=10}\end{array}\right.$ |
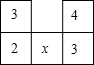 如图所示是由几个相同的小正方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体从正面看和从左面看到的图形,其中x是平方等于本身的正整数.
如图所示是由几个相同的小正方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体从正面看和从左面看到的图形,其中x是平方等于本身的正整数.