题目内容
20.矩形的两条对角线所夹的锐角为60°,较短的边长为12,则对角线长为24.分析 由矩形的性质得出OA=OB,证明△AOB是等边三角形,得出OA=OB=AB=12,即可得出对角线的长.
解答 解:如图所示:
∵四边形ABCD是矩形,
∴OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=12,
∴AC=BD=24.
故答案为:24.
点评 本题考查了矩形的性质、等边三角形的判定与性质;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
5.下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )
| A. | 1,2,3 | B. | 2,2,4 | C. | 1,2,4 | D. | 3,4,5 |
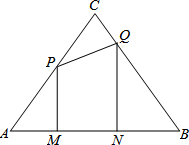 如图,等边三角形ABC的边长为8cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、N.设P、Q两点运动时间为t秒(0<t<4),四边形MNQP的面积为Scm2.
如图,等边三角形ABC的边长为8cm,动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、N.设P、Q两点运动时间为t秒(0<t<4),四边形MNQP的面积为Scm2.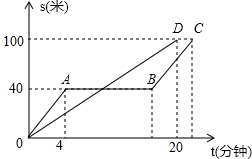 同学们都非常熟悉“龟兔赛跑”的故事,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
同学们都非常熟悉“龟兔赛跑”的故事,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题. 如图,已知三角形ABC及三角形ABC外一点A′,平移三角形ABC,使A点移动到点A′,并保留作图痕迹.
如图,已知三角形ABC及三角形ABC外一点A′,平移三角形ABC,使A点移动到点A′,并保留作图痕迹.