题目内容
8.如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON=35°(直接写出结果).
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON=$\frac{1}{2}α$(直接写出结果).
(4)从(1)(2)(3)的结果中,你能看出什么规律?
分析 (1)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(2)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(3)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(4)由前三个即可得出结论.
解答 解:(1)如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC=75°,∠NOC=$\frac{1}{2}$∠BOC=30°
∴∠MON=∠MOC-∠NOC=45°.
(2)如图2,
∵∠AOB=70°,∠BOC=60°,
∴∠AOC=70°+60°=130°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC=65°,∠NOC=$\frac{1}{2}$∠BOC=30°
∴∠MON=∠MOC-∠NOC=65°-30°=35°.
故答案为:35°.
(3)如图3,∠MON=$\frac{1}{2}$α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(α+β),
∠NOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$β,
∴∠AON=∠AOC-∠NOC=α+β-$\frac{1}{2}$β=α+$\frac{1}{2}$β.
∴∠MON=∠MOC-∠NOC
=$\frac{1}{2}$(α+β)-$\frac{1}{2}$β=$\frac{1}{2}$α
即∠MON=$\frac{1}{2}$α,
故答案为:$\frac{1}{2}$α.
(4)∠MON=$\frac{1}{2}$∠AOB,与∠BOC的大小无关.
点评 本题考查了角平分线定义和角的有关计算,关键是求出∠AOC、∠MOC、∠NOC的度数和得出∠MON=∠MOC-∠NOC

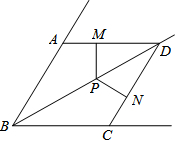 如图,已知在∠ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:
如图,已知在∠ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证: 如图△ABC的三个顶点在网格中格点上,求sinA=$\frac{3}{5}$.
如图△ABC的三个顶点在网格中格点上,求sinA=$\frac{3}{5}$.
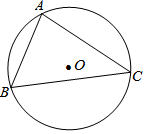 如图,△ABC内接于⊙O,若⊙O的半径为6,∠B=60°,求AC的长.
如图,△ABC内接于⊙O,若⊙O的半径为6,∠B=60°,求AC的长.