题目内容
20.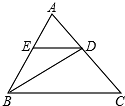 如图,在△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=55°,∠BDC=95°,求△BDE各内角的度数.
如图,在△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=55°,∠BDC=95°,求△BDE各内角的度数.
分析 根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠ABD,再根据角平分线的定义可得∠DBC=∠ABD,然后根据两直线平行,内错角相等可得∠BDE=∠DBC,最后利用三角形的内角和定理列式计算求出∠BED.
解答 解:∵∠A=55°,∠BDC=95°,
∴∠ABD=95°-55°=40°,
∵BD是∠ABC的角平分线,
∴∠DBC=∠ABD=40°,
∵DE∥BC,
∴∠BDE=∠DBC=40°,
在△BDE中,∠BED=180°-∠BDE-∠ABD=180°-40°-40°=100°.
点评 本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
 如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )| A. | 50° | B. | 100° | C. | 45° | D. | 30° |
8. 如图,把一块直角三角板的直角顶点放在一个长方形纸片的一条边上,若∠1=36°,则∠2等于( )
如图,把一块直角三角板的直角顶点放在一个长方形纸片的一条边上,若∠1=36°,则∠2等于( )
 如图,把一块直角三角板的直角顶点放在一个长方形纸片的一条边上,若∠1=36°,则∠2等于( )
如图,把一块直角三角板的直角顶点放在一个长方形纸片的一条边上,若∠1=36°,则∠2等于( )| A. | 34° | B. | 44° | C. | 54° | D. | 64° |
10. 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
 某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )
某校随机抽取200名学生,对他们喜欢的图书类型进行问卷调查,统计结果如图.根据图中信息,估计该校2000名学生中喜欢文学类书籍的人数是( )| A. | 800 | B. | 600 | C. | 400 | D. | 200 |
 如图,已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE,则∠E=30°.
如图,已知△ABC为等边三角形,BD为中线,延长BC至E,使CE=CD,连接DE,则∠E=30°.