Question

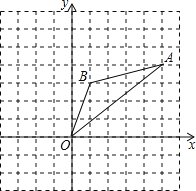
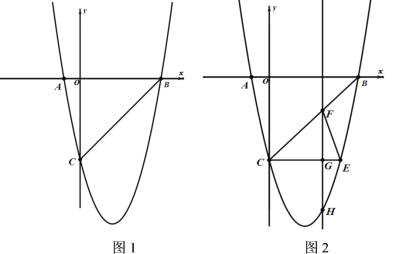
【题目】如图1，在平面直角坐标系中，已知抛物线y=ax2+bx-5与x轴交于A(-1，0)，B(5，0)两点，与y轴交与点C.

(1)求抛物线的函数表达式;

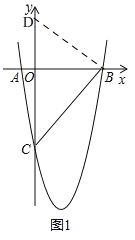
(2)若点D是y轴上的点，且以B、C、D为顶点的三角形与△ABC相似，求点D的坐标;

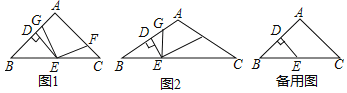
(3)如图2，CE//x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC、CE分别相交于点F，G，试探求当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标及最大面积.

Answer 1

【答案】(1)y=x2-4x-5；(2)D点坐标为(0，1)或(0，)；(3)H(，)；四边形CHEF的最大面积为.

【解析】

（1）根据待定系数法直接确定出抛物线解析式；
（2）分两种情况，利用相似三角形的比例式即可求出点D的坐标；
（3）先求出直线BC的解析式，进而求出四边形CHEF的面积的函数关系式，即可求出最大值；

解：(1)把A(-1，0)，B(5，0)代入y=ax2+bx-5可得

，解得

二次函数的解析式为y=x2-4x-5.

(2) 如图1,令x=0，则y=5，

∴C(0,5)，

∴OC=OB，

∴∠OBC=∠OCB=45°，

∴AB=6,BC=5，

要使以B,C,D为顶点的三角形与△ABC相似,则有或，

当时，

CD=AB=6，

∴D(0,1)，

当时，

∴，

∴CD=，

∴D(0, )，

即：D的坐标为(0,1)或(0, )；

(3)设H(t，t2-4t-5)

∥x轴， ，

又因为点E在抛物线上，即 ，解得（舍去）

∴BC所在直线解析式为y=x-5,

∴ 则，

而CE是定值，

∴当HF的值最大时，四边形CHEF有最大面积。

当时，HF取得最大值，四边形CHEF的最大面积为

,

此时H(，)