题目内容
如图，已知半圆的直径AB=2a，C、D把弧AB三等分，则阴影部分的面积为
- A.
- B.
- C.
- D.
D
分析：连接CD、OD、OC，则阴影部分的面积=S△ADC+S弓形CD，证两三角形全等，然后把阴影部分的面积转为求扇形的面积依面积公式计算即可．
解答：
解：连接CD、OD、OC，
则阴影部分的面积=S△ADC+S弓形CD
∵C、D把弧AB三等份，
∴∠DOC=60°∠DAC=30°，
∵OD=OC=OA=OB，
∴△ODC、△OAD、△OBC是等边三角形，
∴AD∥OC，
∴△ODC、△OAD等底等高，
∴阴影面积=扇形OCD的面积=
=
．
故选D．
点评：本题的关键是分析阴影部分的面积是由哪几部分是组成的，然后根据面积公式计算．
分析：连接CD、OD、OC，则阴影部分的面积=S△ADC+S弓形CD，证两三角形全等，然后把阴影部分的面积转为求扇形的面积依面积公式计算即可．
解答：
解：连接CD、OD、OC，则阴影部分的面积=S△ADC+S弓形CD
∵C、D把弧AB三等份，
∴∠DOC=60°∠DAC=30°，
∵OD=OC=OA=OB，
∴△ODC、△OAD、△OBC是等边三角形，
∴AD∥OC，
∴△ODC、△OAD等底等高，
∴阴影面积=扇形OCD的面积=
=．故选D．
点评：本题的关键是分析阴影部分的面积是由哪几部分是组成的，然后根据面积公式计算．
练习册系列答案
相关题目
如图，已知半圆的直径AB=12cm，点C、D是这个半圆的三等分点，求弦AC、AD有弧CD围成的阴影部分的面积．（结果用π表示）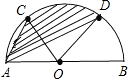
如图，已知半圆的直径AB=4cm，点C、D是这个半圆的三等分点，则弦AC、AD和
如图，已知半圆的直径AB=2a，C、D把弧AB三等分，则阴影部分的面积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
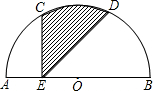如图，已知半圆的直径AB=2a，C、D把弧AB三等分，E是直径上任意一点，则阴影部分的面积为
.