题目内容
3.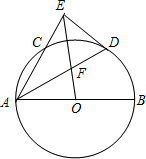 已知线段AB为⊙O的直径,线段AC为⊙O的弦,∠CAB的角平分线交⊙O于点D,过D作DE⊥AC,交AC的延长线于E.
已知线段AB为⊙O的直径,线段AC为⊙O的弦,∠CAB的角平分线交⊙O于点D,过D作DE⊥AC,交AC的延长线于E.(1)求证:DE为⊙O的切线.
(2)连接OE交AD于F,若AE=8,$\frac{AF}{AD}$=$\frac{8}{13}$,求线段AD的长.
分析 (1)连接OD,BC,根据∠CAB的平分线交⊙O于点D,则$\widehat{CD}$=$\widehat{BD}$,依据垂径定理可以得到:OD⊥BC,然后根据直径的定义,可以得到OD∥AE,从而证得,DE⊥OD,则DE是圆的切线;
(2)连接BD,由OD∥AE,证得△AEF∽△DOF,由相似三角形的性质可得OD,再利用相似三角形的判定定理证得△ADE∽△ABD,利用相似三角形的性质可得AD.
解答 (1)证明:连接OD,BC,如图1,
∵∠CAB的平分线交⊙O于点D,
∴∠CAD=∠BAD,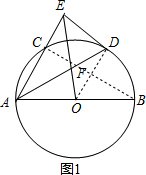
∴$\widehat{CD}$=$\widehat{BD}$,
∴OD⊥BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∵DE⊥AC,
∴DE∥BC,
∴OD⊥DE,
∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)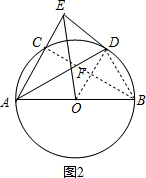 解:连接BD,如图2,
解:连接BD,如图2,
∵$\frac{AF}{AD}$=$\frac{8}{13}$,
∴$\frac{AF}{FD}=\frac{8}{5}$,
∵OD∥AE,
∴△AEF∽△DOF,
∴$\frac{AE}{OD}=\frac{AF}{DF}$,
即$\frac{8}{OD}=\frac{8}{5}$,
∴OD=5,
∴AB=10,
∵AB为直径,
∴∠ADB=90°,∴∠AED=∠ADB,
∵∠CAD=∠DAB,
∴△ADE∽△ABD,
∴$\frac{AD}{AB}=\frac{AE}{AD}$,
∴$\frac{AD}{10}=\frac{8}{AD}$,
∴AD=4$\sqrt{5}$.
点评 本题主要考查了切线的判定和相似三角形的判定与性质、勾股定理,注意构建直角三角形,掌握切线的判定定理是解答此题的关键.

练习册系列答案
相关题目
18.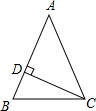 如图,等腰三角形ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
如图,等腰三角形ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
 如图,等腰三角形ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )
如图,等腰三角形ABC中,AB=AC,∠A=50°,CD⊥AB于D,则∠DCB等于( )| A. | 40° | B. | 30° | C. | 23° | D. | 25° |
8.某学校将在体育节举行跳绳活动,为此学校准备购置15米的A种跳绳与3米的B种跳绳若干,已知某商家长、短跳绳的单价如下表
(1)已知购买100条这两种跳绳共花了720元,问A种跳绳买了多少条?
(2)若该商家有一根1000米长的绳子,现将其裁成A、B两种跳绳销售,若销售总价为1300元,求销售后剩余的绳子长度.
| 跳绳种类 | A跳绳 | B跳绳 |
| 单价(单位:元) | 20 | 4 |
(2)若该商家有一根1000米长的绳子,现将其裁成A、B两种跳绳销售,若销售总价为1300元,求销售后剩余的绳子长度.
12. 已知两个数的和为10,设其中较大的一个数为x,它们的积为y.
已知两个数的和为10,设其中较大的一个数为x,它们的积为y.
(1)用函数表达式表示y与x之间的关系;
(2)用表格表示:
(3)用图象表示y与x之间的关系.
 已知两个数的和为10,设其中较大的一个数为x,它们的积为y.
已知两个数的和为10,设其中较大的一个数为x,它们的积为y.(1)用函数表达式表示y与x之间的关系;
(2)用表格表示:
| x | … | ||||||||
| y | … |