��Ŀ����
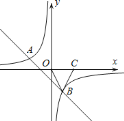
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��x���ཻ��
��x���ཻ��![]() ��C����
��C����![]() ��y���ཻ�ڵ�B
��y���ཻ�ڵ�B![]() ��
��
![]() a0��
a0�� ![]()
![]() �
�![]() ����
����![]() ��
�� ![]() ��
��
![]() ���������߹���ֱ��
���������߹���ֱ��![]() �Գƣ��������ߵĺ�������ʽ��
�Գƣ��������ߵĺ�������ʽ��
![]() ��
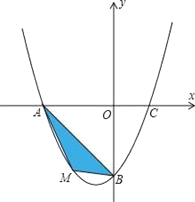
��![]() �������£�����MΪ������������������һ���㣬��M�ĺ�����Ϊ
�������£�����MΪ������������������һ���㣬��M�ĺ�����Ϊ![]() �����Ϊ
�����Ϊ![]() ��S����m�ĺ�����ϵʽ�������S�����ֵ��
��S����m�ĺ�����ϵʽ�������S�����ֵ��
![]() ��
��![]() �������£�����P���������ϵĶ��㣬��Q��ֱ��
�������£�����P���������ϵĶ��㣬��Q��ֱ��![]() �ϵĶ��㣬�ж��м���λ���ܹ�ʹ�Ե�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�ϵĶ��㣬�ж��м���λ���ܹ�ʹ�Ե�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
���𰸡�![]() ��
�� ![]() ����2��
����2��![]() ��
�� ![]() S����m�ĺ�����ϵʽΪ
S����m�ĺ�����ϵʽΪ![]() ��
�� ![]() ʱ��S�����ֵ
ʱ��S�����ֵ![]() ��
�� ![]() ����Ϊ
����Ϊ![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
��![]() ��
��
����������������� ![]() �ɿ������ϣ���֪
�ɿ������ϣ���֪![]() ͼ����
ͼ����![]() �����������㣬��
�����������㣬��![]()
![]() �ɶԳ����֪��
�ɶԳ����֪��![]() ���꣬Ȼ��ѵ�
���꣬Ȼ��ѵ�![]() ��������뺯������ʽ�����ô���ϵ������⼴�ɣ�
��������뺯������ʽ�����ô���ϵ������⼴�ɣ�
![]() ����ͼ�εĸ�����ɵö��κ��������������ߵ�����������������ڶ��κ�������ֵ��Ȼ�ɵý⣻
����ͼ�εĸ�����ɵö��κ��������������ߵ�����������������ڶ��κ�������ֵ��Ȼ�ɵý⣻
![]() �����꣬Ȼ�����
�����꣬Ȼ�����![]() �ij��ȣ��ٸ���ƽ���ı��εĶԱ�����г���ʽ��Ȼ������
�ij��ȣ��ٸ���ƽ���ı��εĶԱ�����г���ʽ��Ȼ������![]() ��һԪ���η��̼��ɵý⣮
��һԪ���η��̼��ɵý⣮
��������� ![]() ��
�� ![]() ��
��
![]() �����߹���ֱ��
�����߹���ֱ��![]() �Գƣ�
�Գƣ� ![]() ��
��
![]()
��![]() ������뺯������ʽ����
������뺯������ʽ����
![]() ��
��
���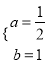 ��
��
���Դ˺�������ʽΪ�� ![]() ��
��
![]() ��ĺ�����Ϊm���ҵ�M�������������ϣ�
��ĺ�����Ϊm���ҵ�M�������������ϣ�
![]() ���������
��������� ![]() ��
��
![]()
![]()
![]()
![]() ��
��
![]() ��
��
��![]() ʱ��S�����ֵΪ��
ʱ��S�����ֵΪ�� ![]() ��
��
��S����m�ĺ�����ϵʽΪ![]() ��
�� ![]() ʱ��S�����ֵ
ʱ��S�����ֵ![]() ��
��
![]() ����Ϊ
����Ϊ![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
��![]() ��
��

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�