题目内容
18.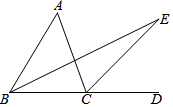 如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.求∠E的度数.
如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.求∠E的度数.
分析 先根据外角定理和∠A=40°,得出∠ACD-∠ABC=40°,再利用角平分线的定义得:$\frac{1}{2}$∠ACD-$\frac{1}{2}$∠ABC=20°,即∠E=∠ECD-∠EBC=20°.
解答 解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠A+∠ABC,
∴∠A=∠ACD-∠ABC,
∵∠A=40°,
∴∠ACD-∠ABC=40°,
∵BE平分∠ABC,CE平分∠ACD,
∴∠ECD=$\frac{1}{2}$∠ACD,∠EBC=$\frac{1}{2}$∠ABC,
∵∠ECD是△BCE的一个外角,
∴∠ECD=∠EBC+∠E,
∴∠E=∠ECD-∠EBC=$\frac{1}{2}$∠ACD-$\frac{1}{2}$∠ABC=20°.
点评 本题考查了三角形的外角性质,同时要运用整体的思想,所以本题对初学几何的学生来说有难度,关键是从∠ACD这个外角看到∠ECD,根据等量代换解决此题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
10.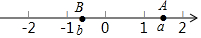 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
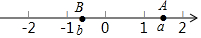 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )| A. | ab>0 | B. | b-a>0 | C. | (a-1)(b-1)>0 | D. | (a-1)(b+1)>0 |