题目内容
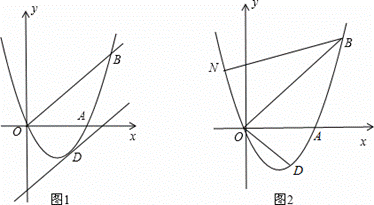
如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足
△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
 |
解:(1)∵抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)
∴将A与B两点坐标代入得: ,解得:
,解得: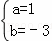 ,
,
∴抛物线的解析式是y=x2﹣3x.
(2)设直线OB的解析式为y=k1x,由点B(4,4),
得:4=4k1,解得:k1=1 ∴直线OB的解析式为y=x,
∴直线OB向下平移m个单位长度后的解析式为:y=x﹣m,
∴x﹣m=x2﹣3x,
 ∵抛物线与直线只有一个公共点, ∴△=16﹣4m=0,
∵抛物线与直线只有一个公共点, ∴△=16﹣4m=0,
解得:m=4,
此时x1=x2=2,y=x2﹣3x=﹣2,
∴D点的坐标为(2,﹣2).
(3)∵直线OB的解析式为y=x,且A(3,0),
∴点A关于直线OB的对称点A′的坐标是(0,3),
根据轴对称性质和三线合一性质得出∠A′BO=∠ABO,
设直线A′B的解析式为y=k2x+3,过点(4,4),
∴4k2+3=4,解得:k2=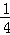 , ∴直线A′B的解析式是y=
, ∴直线A′B的解析式是y= ,
,
∵∠NBO=∠ABO,∠A′BO=∠ABO, ∴BA′和BN重合,即点N在直线A′B上,
∴设点N(n,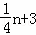 ),又点N在抛物线y=x2﹣3x上,
),又点N在抛物线y=x2﹣3x上,
∴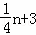 =n2﹣3n, 解得:n1=﹣
=n2﹣3n, 解得:n1=﹣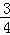 ,n2=4(不合题意,舍去)
,n2=4(不合题意,舍去)
∴N点的坐标为(﹣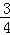 ,
,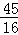 ).
).
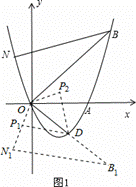
如图1,将△NOB沿x轴翻折,得到△N1OB1,
则N1(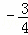 ,
, ),B1(4,﹣4),
),B1(4,﹣4),
∴O、D、B1都在直线y=﹣x上.
∵△P1OD∽△NOB,△NOB≌△N1OB1, ∴△P1OD∽△N1OB1,
∴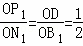 , ∴点P1的坐标为(
, ∴点P1的坐标为(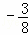 ,
,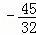 ).
).
将△OP1D沿直线y=﹣x翻折,可得另一个满足条件的点P2(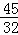 ,
,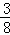 ),
),
综上所述,点P的坐标是( ,
,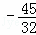 )或(
)或(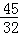 ,
,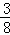 ).
).

 ,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.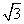 ︰2时,求弧AF的度数;
︰2时,求弧AF的度数;
 是数据3,5,3,9,8中的中位数,求关于x的方程
是数据3,5,3,9,8中的中位数,求关于x的方程
 = .
= .
 B、
B、 C、
C、 D、
D、
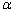 是某直角三角形内角中较大的锐角,
是某直角三角形内角中较大的锐角,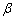 是某五边形的外角中的最大角,甲、乙、丙、丁计算
是某五边形的外角中的最大角,甲、乙、丙、丁计算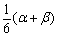 的结果依次为10°、15°、30°、35°,其中有正确的结果,则计算正确的是( )
的结果依次为10°、15°、30°、35°,其中有正确的结果,则计算正确的是( )