题目内容
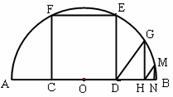
如图,AB是半圆O的直径,且AB=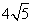 ,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
,矩形CDEF内接于半圆,点C,D在AB上,点E,F在半圆上.
(1)当矩形CDEF相邻两边FC︰CD=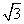 ︰2时,求弧AF的度数;
︰2时,求弧AF的度数;
(2)当四边形CDEF是正方形时:
①试求正方形CDEF的边长;
②若点G,M在⊙O上, GH⊥AB于H,MN⊥AB于N,且△GDH和△MHN都是等腰直角三角形,求HN的长.
解:(1)连结FO,根据圆的对称性,矩形CDEF内接于半圆可得CO=OD,
∴Rt△COF中,FC︰CD=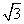 ︰1,∴∠FOC=60°
︰1,∴∠FOC=60°
∴弧AF的度数为60°
(2)① ∵四边形CDEF是正方形,∴FC=2CO -- 分
∵FC2+CO2= ,解得CO=2,∴CF=4,正方形的边长为4
,解得CO=2,∴CF=4,正方形的边长为4
② 连结OG,OM,∵△GDH和△MHN都是等腰直角三角形,∴DH=HG,HN=MN
在Rt△OGH中, ,设DH=x,则
,设DH=x,则
 解得x=2 或x=-4(舍去)
解得x=2 或x=-4(舍去)
在Rt△OMN中, ,设HN=y,
,设HN=y,
∴ ,解得
,解得 (舍去负值)
(舍去负值)
∴

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
某班级学生参加体质健康测试,其中有20名同学参加了排球发球考试,裁判将发球过网个数记入下表,由于不小心弄脏了表格,有两个数据看不到. 则下列说法中正确的是( )
| 过网个数 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 2 | 5 |
A.这组数据众数是8 B.这组数据的中位数是7.5
C.这组数据的方差是4 D.这组数据的平均数P满足8.1<P<8.6

 ),(0,
),(0, 度得到四边形
度得到四边形 ,此时直线
,此时直线 、直线
、直线 分别与直线BC相交于点P、Q.
分别与直线BC相交于点P、Q. 落在
落在 轴正半轴时,旋转角
轴正半轴时,旋转角
 时,存在着这样的点P和点Q,使
时,存在着这样的点P和点Q,使 ,请直接写出点P的坐标 [根据景宁县模拟试卷改编]
,请直接写出点P的坐标 [根据景宁县模拟试卷改编]
 中,
中, .将射线
.将射线 绕着点
绕着点 顺时针旋转
顺时针旋转
 ≤
≤ 得到射线
得到射线 ,点
,点 与点
与点 关于直线
关于直线 ,图中某点到点
,图中某点到点 ,表示
,表示 的函数关系的图象如图2所示,则这个点
的函数关系的图象如图2所示,则这个点 为图1中的( )
为图1中的( ) C. 点
C. 点 D. 点
D. 点


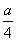 是分数;②a可以用数轴上的一个点来表示;③3<a<4;④a是8的算术平方根。其中所有正确说法的序号是( )
是分数;②a可以用数轴上的一个点来表示;③3<a<4;④a是8的算术平方根。其中所有正确说法的序号是( )