题目内容
19. 已知:如图.在△ABC中.AB=AC.∠B=30°,DA⊥AC.求证:CD=2BD.
已知:如图.在△ABC中.AB=AC.∠B=30°,DA⊥AC.求证:CD=2BD.
分析 根据AB=AC可知∠B与∠C的关系,由∠B=30°可知∠C的度数,由∠BAC=120°,又由DA⊥AC,可得∠BAD的度数,由∠C=30°,可得CD与AD的关系,从而可以得到CD与BD的关系.
解答 证明:∵在△ABC中.AB=AC.∠B=30°,
∴∠B=∠C=30°,∠BAC=120°.
又∵DA⊥AC,
∴∠DAC=90°.
∴∠BAD=∠BAC-∠DAC=30°.
∵∠DAC=90°,∠C=30°,
∴CD=2BD.
∵∠B=∠BAD=30°,
∴AD=BD.
∴CD=2BD.
点评 本题考查三角形的内角和和在直角三角形中30°角所对的直角边与斜边的关系,关键是明确题意,进行正确的分析,最终得出结论.

练习册系列答案
相关题目
4.若□-(-3)=4,则□表示的数( )
| A. | -1 | B. | 1 | C. | 7 | D. | -7 |
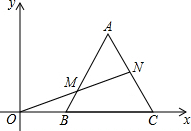 如图,在平面直角坐标系中,等边三角形ABC的顶点B、C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M.当边AB恰平分线段ON时,则AN=2.
如图,在平面直角坐标系中,等边三角形ABC的顶点B、C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M.当边AB恰平分线段ON时,则AN=2.