Question

在平面直角坐标系中，O为原点，直线y =－2x－1与y轴交于点A，与直线y =－x交于点B, 点B关于原点的对称点为点C.

（1）求过A，B，C三点的抛物线的解析式；

（2）P为抛物线上一点，它关于原点的对称点为Q.

①当四边形PBQC为菱形时，求点P的坐标；

②若点P的横坐标为t（－1＜t＜1），当t为何值时，四边形PBQC面积最大，并说明理由.

Answer 1

解：（1）解方程组得

∴点B的坐标为（-1，1）.························ 1分

∵点C和点B关于原点对称，

∴点C的坐标为（1，-1）.························ 2分

又∵点A是直线y=-2x-1与y轴的交点，

∴点A的坐标为（0，-1）.························ 3分

设抛物线的解析式为y=ax²+bx+c，

∴解得

∴抛物线的解析式为y=x²-x-1.······················ 5分

（2）①如图1，∵点P在抛物线上，

∴可设点P的坐标为（m，m²-m-1）.

当四边形PBQC是菱形时，O为菱形的中心，

∴PQ⊥BC，即点P，Q在直线y = x上，

∴m = m²-m-1，····························· 7分

解得m = 1±.···························· 8分

∴点P的坐标为（1+，1+）或（1-，1-）.··········· 9分

 

图1                                      图2

②方法一：

如图2，设点P的坐标为（t，t² - t - 1）.

过点P作PD∥y轴，交直线y = - x于点D，则D（t，- t）.

分别过点B，C作BE⊥PD，CF⊥PD，垂足分别为点E，F.

∴PD = - t -( t² - t -1) = - t² + 1，BE + CF = 2，··········· 10分

∴S_△PBC＝PD·BE +PD·CF

＝PD·（BE + CF）

＝（- t² + 1）×2

＝- t² + 1.··························· 12分

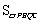∴＝-2t²+2.

∴当t＝0时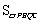，有最大值2. ···················· 13分

方法二：

如图3，过点B作y轴的平行线，过点C作x轴的平行线，两直线交于点D，连接PD.

∴S_△PBC＝S_△BDC-S_△PBD-S_△PDC

＝×2×2-×2（t+1）-×2（t²-t-1+1）

＝-t²+1.···························· 12分

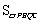∴＝-2t²+2.

∴当t＝0时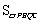，有最大值2. ···················· 13分

 

图3                                   图4

方法三：如图4，过点P作PE⊥BC，垂足为E，作PF∥x轴交BC于点F.

∴PE=EF.

∵点P的坐标为（t，t²-t-1），

∴点F的坐标为（-t²+t+1，t²-t-1）.

∴PF=-t²+t+1-t=-t²+1.

∴PE＝（-t²+1）.·························· 11分

∴S_△PBC＝BC·PE＝××（-t²+1）

＝-t²+1.···························· 12分

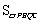∴＝-2t²+2.

∴当t＝0时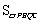，有最大值2.