Question

【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

（1）概念理解

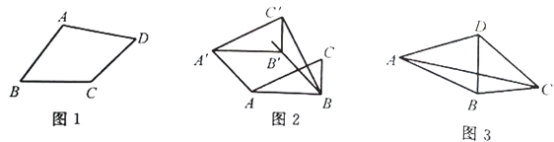
如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．

（2）问题探究

①小红猜想：对角线互相平分的“等邻边四边形”是菱形．她的猜想正确吗？请说明理由．

②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿∠ABC的平分线BB＇方向平移得到△A＇B＇C＇，连结AA＇，BC＇．小红要是平移后的四边形ABC＇A＇是“等邻边四边形”，应平移多少距离（即线段BB＇的长）？

（3）应用拓展

如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD==90°，AC，BD为对角线，AC=AB．试探究BC，CD，BD的数量关系．

Answer 1

【答案】（1）AB=BC或BC=CD或CD=AD或AD=AB（任写一个即可）；

（2）①正确，理由见解析②2或或或；

（3）BC2+CD2=2BD2，理由见解析

【解析】

试题（1）由“等邻边四边形”的定义易得出结论；

（2）①先利用平行四边形的判定定理得平行四边形，再利用“等邻边四边形”定义得邻边相等，得出结论；

②由平移的性质易得BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC=，再利用“等邻边四边形”定义分类讨论，由勾股定理得出结论；

（3）由旋转的性质可得△ABF≌△ADC，由全等性质得∠ABF=∠ADC，∠BAF=∠DAC，AF=AC，FB=CD，利用相似三角形判定得△ACF∽△ABD，由相似的性质和四边形内角和得∠CBF=90°，利用勾股定理，等量代换得出结论．

试题解析：（1）AB=BC或BC=CD或CD=AD或AD=AB（任写一个即可）；

（2）①正确，理由为：

∵四边形的对角线互相平分，∴这个四边形是平行四边形，

∵四边形是“等邻边四边形”，∴这个四边形有一组邻边相等，

∴这个“等邻边四边形”是菱形；

②∵∠ABC=90°，AB=2，BC=1，

∴AC=，

∵将Rt△ABC平移得到△A′B′C′，

∴BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC=，

（I） 如图1，当AA′=AB时，BB′=AA′=AB=2；

（II） 如图2，当AA′=A′C′时，BB′=AA′=A′C′=；

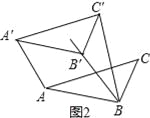
（III）当A′C′=BC′=时，

如图3，延长C′B′交AB于点D，则C′B′⊥AB，

∵BB′平分∠ABC，

∴∠ABB′=∠ABC=45°，

∴∠BB′D=′∠ABB′=45°

∴B′D=B，

设B′D=BD=x，

则C′D=x+1，BB′=x，

∵在Rt△BC′D中，BD2+（C′D）2=（BC′）2

∴x2+（x+1）2=（）2，

解得：x1=1，x2=﹣2（不合题意，舍去），

∴BB′=x=

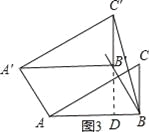
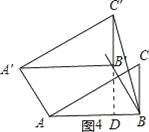
（Ⅳ）当BC′=AB=2时，如图4，与（Ⅲ）方法一同理可得：BD2+（C′D）2=（BC′）2，

设B′D=BD=x，

则x2+（x+1）2=22，

解得：x1=，x2=（不合题意，舍去），

∴BB′=x=；

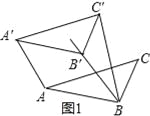
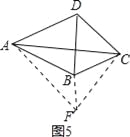
（3）BC，CD，BD的数量关系为：BC2+CD2=2BD2，如图5，

∵AB=AD，

∴将△ADC绕点A旋转到△ABF，连接CF，

∴△ABF≌△ADC，

∴∠ABF=∠ADC，∠BAF=∠DAC，AF=AC，FB=CD，

∴∠BAD=∠CAF，=1，

∴△ACF∽△ABD，

∴=，∴CF=BD，

∵∠BAD+∠ADC+∠BCD+∠ABC=360°，

∴∠ABC+∠ADC﹣360°﹣（∠BAD+∠BCD）=360°﹣90°=270°，

∴∠ABC+∠ABF=270°，

∴∠CBF=90°，

∴BC2+FB2=CF2=（BD）2=2BD2，

∴BC2+CD2=2BD2．