ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌжБЯпy=![]()
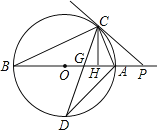
![]() x+8гыxжсНЛгкAЕуЃЌгыyжсНЛгкЕуBЃЌЖЏЕуPДгAЕуГіЗЂЃЌвдУПУы2ИіЕЅЮЛЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌЭЌЪБЖЏЕуQДгBЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпBAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЕБвЛИіЕуЭЃжЙдЫЖЏЃЌСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЌСЌНгPQЃЌЩшдЫЖЏЕФЪБМфЮЊtЃЈУыЃЉЃЎ
x+8гыxжсНЛгкAЕуЃЌгыyжсНЛгкЕуBЃЌЖЏЕуPДгAЕуГіЗЂЃЌвдУПУы2ИіЕЅЮЛЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌЭЌЪБЖЏЕуQДгBЕуГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпBAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЕБвЛИіЕуЭЃжЙдЫЖЏЃЌСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЌСЌНгPQЃЌЩшдЫЖЏЕФЪБМфЮЊtЃЈУыЃЉЃЎ
ЃЈ1ЃЉгУtЕФДњЪ§ЪНБэЪОAP= ЃЌAQ=
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌPQЁЮOBЃП
ЃЈ3ЃЉШєЕуCЮЊЦНУцжБНЧзјБъЯЕФквЛЕуЃЌЪЧЗёДцдкtжЕЃЌЪЙЕУвдAЁЂPЁЂQЁЂCЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃПШєДцдкЃЌЧѓГіQЕузјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЕу
ЃЛЃЈ3ЃЉЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌЯШЧѓГіЕуAКЭЕуBЕФзјБъЃЌЕУЕНABЕФГЄЖШЃЌИљОнТЗГЬ=ЫйЖШ![]() ЪБМфЃЌМДПЩБэЪОГіAPКЭBQЃЛ
ЪБМфЃЌМДПЩБэЪОГіAPКЭBQЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊAPКЭAQЃЌШЛКѓРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЃЌМДПЩЧѓГіtЕФжЕЃЛ
ЃЈ3ЃЉЗжШ§жжЧщаЮСаГіЗНГЬЧѓНтЃКЂйЕБ![]() ЃЌзї
ЃЌзї![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУСтаЮ
ЃЌПЩЕУСтаЮ![]() ЃЛЂкЕБ
ЃЛЂкЕБ![]() ЪБЃЌзї
ЪБЃЌзї![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУСтаЮ
ЃЌПЩЕУСтаЮ![]() ЃЛЂлЕБ
ЃЛЂлЕБ![]() ЪБЃЌзї
ЪБЃЌзї![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУСтаЮ
ЃЌПЩЕУСтаЮ![]() ЃЛЗжБ№ЧѓГіЕуQЕФзјБъМДПЩ.
ЃЛЗжБ№ЧѓГіЕуQЕФзјБъМДПЩ.
НтЃКЃЈ1ЃЉИљОнЬтвтЃЌСю![]() ЃЌдђ
ЃЌдђ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
Сю![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЕу![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
дк![]() жаЃЌгЩЙДЙЩЖЈРэЕУЃЌ
жаЃЌгЩЙДЙЩЖЈРэЕУЃЌ![]() ЃЌ
ЃЌ
ЁпЕу![]() ЕФЫйЖШЪЧУПУы2ИіЕЅЮЛЃЌЕу
ЕФЫйЖШЪЧУПУы2ИіЕЅЮЛЃЌЕу![]() ЕФЫйЖШЪЧУПУы1ИіЕЅЮЛЃЌ
ЕФЫйЖШЪЧУПУы1ИіЕЅЮЛЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌШчЭМЃК
ЃЌШчЭМЃК
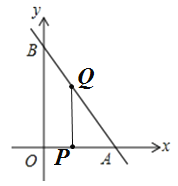
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйШчЭМжаЃЌЕБ![]() ЃЌзї
ЃЌзї![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУСтаЮ
ЃЌПЩЕУСтаЮ![]() ЃЎ
ЃЎ
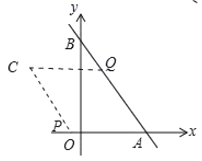
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЩшЕуQЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрДЫЪБ![]() ЃЛ
ЃЛ
ЂкШчЭМжаЃЌЕБ![]() ЪБЃЌзї
ЪБЃЌзї![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУСтаЮ
ЃЌПЩЕУСтаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гк
гк![]() ЃЎ
ЃЎ
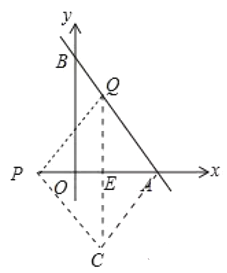
ЁпЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
гыЂйЭЌРэПЩЧѓЕуQЕФзјБъЃЌ
ЁрДЫЪБ![]() ЃЎ
ЃЎ
ЂлШчЭМжаЃЌЕБ![]() ЪБЃЌзї
ЪБЃЌзї![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУСтаЮ
ЃЌПЩЕУСтаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гк
гк![]() ЃЎ
ЃЎ
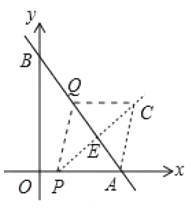
ЁпЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр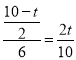 ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
гыЂйЭЌРэПЩЧѓЕуQЕФзјБъЃЌ
ЁрДЫЪБ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕу![]() ЕФзјБъЮЊЃК
ЕФзјБъЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ

 ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ
ЬиИпМЖНЬЪІЕуВІЯЕСаД№АИ