题目内容
20.计算:(1+$\sqrt{2}$-$\sqrt{3}$)2•(1-$\sqrt{2}$+$\sqrt{3}$)2.分析 先变形得到原式={[1+($\sqrt{2}$-$\sqrt{3}$)]•[1-($\sqrt{2}$-$\sqrt{3}$)]}2,然后根据平方差公式计算,利用完全平方公式进行.
解答 解:原式=[(1+$\sqrt{2}$-$\sqrt{3}$)•(1-$\sqrt{2}$+$\sqrt{3}$)]2
={[1+($\sqrt{2}$-$\sqrt{3}$)]•[1-($\sqrt{2}$-$\sqrt{3}$)]}2
=[12-($\sqrt{2}$-$\sqrt{3}$)2]2
=(1-5+2$\sqrt{6}$)2
=(2$\sqrt{6}$-4)2
=24-16$\sqrt{6}$+16
=40-16$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
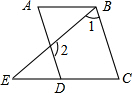 如图,已知∠A=∠C,∠1与∠2互补,
如图,已知∠A=∠C,∠1与∠2互补,