题目内容
方程x2-6x+k=0的一根是4，则k= ，另一个根是 ．
考点：一元二次方程的解,根与系数的关系
专题：
分析：将x=4代入已知方程，列出关于k的新方程，通过解新方程来求k的值即可．由根与系数的关系来求方程的另一根．
解答：解：设方程x2-6x+k=0的另一根为t，则
t+4=6，
解得 t=2．
把x=4代入方程，得
42-6×4+k=0，
解得k=8．
故答案是：8；2．
t+4=6，
解得 t=2．
把x=4代入方程，得
42-6×4+k=0，
解得k=8．
故答案是：8；2．
点评：本题考查的是一元二次方程的根即方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
练习册系列答案
一线名师权威作业本系列答案
相关题目
计算20022-2001×2003的结果是（ ）
| A、1 | B、-1 | C、2 | D、-2 |
如图，矩形ABCD中，AB=3，AD=5．将矩形ABCD在直线l上按顺时针方向不滑动地每秒转动90°，转动3秒后停止，则顶点A经过的路线长为
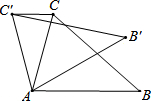如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=（ ）| A、30° | B、35° |
| C、40° | D、50° |
