题目内容
6. 二次函数y=2$\sqrt{3}$x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=2$\sqrt{3}$x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积是$\frac{9\sqrt{3}}{2}$.
二次函数y=2$\sqrt{3}$x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=2$\sqrt{3}$x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积是$\frac{9\sqrt{3}}{2}$.
分析 连结BC交OA于D,如图,根据菱形的性质得BC⊥OA,∠OBD=60°,利用含30度的直角三角形三边的关系得OD=$\sqrt{3}$BD,设BD=t,则OD=$\sqrt{3}$t,B(t,$\sqrt{3}$t),利用二次函数图象上点的坐标特征得$\frac{2}{3}$$\sqrt{3}$t2=$\sqrt{3}$t,解得t1=0(舍去),t2=$\frac{3}{2}$,则BD=1,OD=$\sqrt{3}$,然后根据菱形性质得BD=$\frac{3}{2}$,OD=$\frac{3\sqrt{3}}{2}$,BC=2BD=3,OA=2OD=3$\sqrt{3}$,再利用菱形面积公式计算即可.
解答 解:连结BC交OA于D,如图,
∵四边形OBAC为菱形,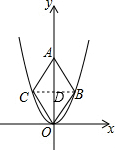
∴BC⊥OA,
∵∠OBA=120°,
∴∠OBD=60°,
∴OD=$\sqrt{3}$BD,
设BD=t,则OD=$\sqrt{3}$t,
∴B(t,$\sqrt{3}$t),
把B(t,$\sqrt{3}$t)代入y=$\frac{2}{3}$$\sqrt{3}$x2得$\frac{2}{3}$$\sqrt{3}$t2=$\sqrt{3}$t,
解得t1=0(舍去),t2=$\frac{3}{2}$,
∴BD=$\frac{3}{2}$,OD=$\frac{3\sqrt{3}}{2}$,
∴BC=2BD=3,OA=2OD=3$\sqrt{3}$,
∴菱形OBAC的面积=$\frac{1}{2}$×3×3$\sqrt{3}$=$\frac{9}{2}$$\sqrt{3}$.
故答案为:$\frac{9\sqrt{3}}{2}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形面积=$\frac{1}{2}$ab(a、b是两条对角线的长度).也考查了二次函数图象上点的坐标特征.

| A. | 36° | B. | 54° | C. | 64° | D. | 90° |
 如图,∠1和∠2是直线BE、DF被直线BC截得的同位角,∠3与∠4是直线BE、DF被直线EF截得的内错角.
如图,∠1和∠2是直线BE、DF被直线BC截得的同位角,∠3与∠4是直线BE、DF被直线EF截得的内错角.

 如图,圆锥的轴截面是边长为9cm的正三角形ABC,P是母线AC的中点.求在圆锥的侧面上从B点到P点的最短路线的长.
如图,圆锥的轴截面是边长为9cm的正三角形ABC,P是母线AC的中点.求在圆锥的侧面上从B点到P点的最短路线的长.