Question

如图，在Rt△ABC中，∠ACB=90°，AC=5cm，BC=12cm，将△ABC绕点B顺时针旋转60°，得到△BDE，连接DC交AB于点F，则△ACF与△BDF的周长之和为　　　　　　cm．

Answer 1

　42　cm．

【考点】旋转的性质．

【分析】根据将△ABC绕点B顺时针旋转60°，得到△BDE，可得△ABC≌△BDE，∠CBD=60°，BD=BC=12cm，从而得到△BCD为等边三角形，得到CD=BC=CD=12cm，在Rt△ACB中，利用勾股定理得到AB=13，所以△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD，即可解答．

【解答】解：∵将△ABC绕点B顺时针旋转60°，得到△BDE，

∴△ABC≌△BDE，∠CBD=60°，

∴BD=BC=12cm，

∴△BCD为等边三角形，

∴CD=BC=CD=12cm，

在Rt△ACB中，AB=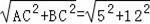=13，

△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=5+13+12+12=42（cm），

故答案为：42．