题目内容
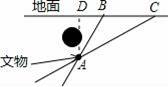
如图所示,某古代文物被探明埋于地下的A处,由于点A上方有一些管道,考古人员不能垂直向下挖掘,他们被允许从B处或C处挖掘,从B处挖掘时,最短路线BA与地面所成的锐角是56°,从C处挖掘时,最短路线CA与地面所成的锐角是30°,且BC=20m,若考古人员最终从B处挖掘,求挖掘的最短距离.(参考数据:sin56°=0.83,tan56°≈1.48,
 ≈1.73,结果保留整数)
≈1.73,结果保留整数)


【考点】解直角三角形的应用.
【分析】作AD⊥BC交CB延长线于点D,执行额AD即为文物在地面下的深度.设AD=x.通过解直角△ABD求得BD=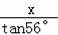
 ;通过解直角△ACD求得CD=
;通过解直角△ACD求得CD=
 x,由此列出关于x的方程,通过方程求得AD的长度.最后通过解直角三角形ABD来求AB的长度即可.
x,由此列出关于x的方程,通过方程求得AD的长度.最后通过解直角三角形ABD来求AB的长度即可.
【解答】解:作AD⊥BC交CB延长线于点D,执行额AD即为文物在地面下的深度.
根据题意得∠CAD=30°,∠ABD=56°.
设AD=x.
在直角△ABD中,∵∠ABD=56°,
∴BD=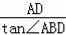
 =
=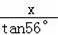
 .
.
在直角△ACD中,∵∠ACB=30°,
∴CD=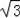
 AD=
AD=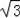
 x,
x,
∴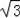
 x=
x=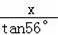
 +20.
+20.
解得x≈18.97,
∴AB=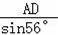
 ≈
≈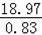
 ≈23.
≈23.
答:从B处挖掘的最短距离为23米.

【点评】此题考查了解直角三角形的应用,主要是正切、余弦概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

 a-b)2+5a(a-b),其中
a-b)2+5a(a-b),其中 .
.


 ÷
÷
 ﹣
﹣
 ,其中a=
,其中a=

 ﹣
﹣
 )÷
)÷
 ,并从﹣1≤x≤2中选一个你认为合适的整数x代入求值.
,并从﹣1≤x≤2中选一个你认为合适的整数x代入求值.


 D.4
D.4