题目内容
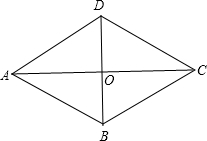如图，?ABCD的对角线AC，BD相交于点O，且AB=10，AO=8，BO=6，求证?ABCD的菱形．考点：菱形的判定,平行四边形的性质
专题：证明题
分析：首先利用勾股定理逆定理证明AC⊥BD，再根据对角线互相垂直的平行四边形是菱形可证明结论．
解答：证明：∵四边形ABCD是平行四边形，
∵62+82=102，
∴AO2+BO2=AB2，
∴∠AOB=90°，
∴AC⊥BD，
∵四边形ABCD是平行四边形，
∴?ABCD的菱形．
∵62+82=102，
∴AO2+BO2=AB2，
∴∠AOB=90°，
∴AC⊥BD，
∵四边形ABCD是平行四边形，
∴?ABCD的菱形．
点评：此题主要考查了菱形的判定，关键是掌握对角线互相垂直的平行四边形是菱形．
练习册系列答案
阅读快车系列答案
相关题目
小明参加班长竞选，需进行演讲答辩与民主测评，民主测评时一人一票，按“优秀、良好、一般”三选一投票．如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图．根据统计图表中的数据和评分规则，本次竞选中小明的综合得分数为（ ）
| A、85 | B、85.2 |
| C、85.3 | D、85.5 |
如图，在Rt△ABC中，∠C=90°，ED是线段AB的垂直平分线，∠A=下列四个函数中，当x＞0时，y随x的增大而增大的是（ ）
| A、y=-3x | ||
| B、y=-x-1 | ||
C、y=-
| ||
D、y=
|
下面的多项式中，能因式分解的是（ ）
| A、m2+n2 |
| B、m2-nm+n |
| C、m2-n4 |
| D、m2-n |