题目内容
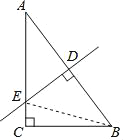
如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分线分别交AB、AC于点D、E,
(1)求AB的长度;
(2)求CE的长.
练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
题目内容
如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分线分别交AB、AC于点D、E,
(1)求AB的长度;
(2)求CE的长.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案