题目内容
3.抛物线y=-(x+1)2-2与抛物线y=(x+1)2+2关于x轴成轴对称;抛物线y=-(x+1)2-2与抛物线y=-(x-1)2-2关于y轴成轴对称.分析 由关于x轴对称点的特点是:横坐标不变,纵坐标变为相反数,可求出抛物线y=-(x+1)2-2关于x轴对称的抛物线解析式;再由关于y轴对称点的特点是:纵坐标不变,横坐标变为相反数,可得关于y轴对称的抛物线解析式.
解答 解:∵y=-(x+1)2-2,
∴关于x轴对称的抛物线解析式为-y=-(x+1)2-2,即y=(x+1)2+2;
∴关于y轴对称的抛物线解析式为y=-(-x+1)2-2,即y=-(x-1)2-2.
故答案为y=(x+1)2+2;y=-(x-1)2-2.
点评 此题考查了二次函数的图象与几何变换,解题的关键是抓住关于x轴、y轴对称点的特点.

练习册系列答案
相关题目
13.为了了解某校八年级1 000名学生的身高,从中抽取了50名学生并对他们的身高进行统计分析,在这个问题中,总体是指( )
| A. | 1 000名学生 | B. | 被抽取的50名学生 | ||
| C. | 1 000名学生的身高 | D. | 被抽取的50名学生的身高 |
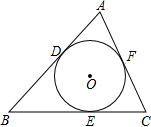 如图,⊙O是△ABC的内切圆,切点分别为D,E,F.若AB=6,BC=5,AC=4,求AD,CF.
如图,⊙O是△ABC的内切圆,切点分别为D,E,F.若AB=6,BC=5,AC=4,求AD,CF. 已知二次函数图象的顶点是(-1,2),且过点$({0,\frac{3}{2}})$.
已知二次函数图象的顶点是(-1,2),且过点$({0,\frac{3}{2}})$.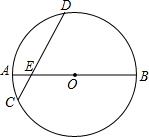 如图所示,已知⊙O的直径AB和弦CD相交于点E,AE=1cm,BE=5cm,∠BED=60°,求DE的长.
如图所示,已知⊙O的直径AB和弦CD相交于点E,AE=1cm,BE=5cm,∠BED=60°,求DE的长.