题目内容
【题目】（题文）
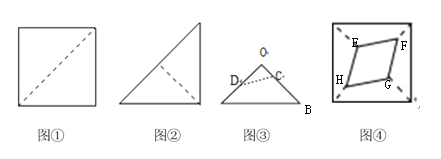
将一张正方形纸片按如图步骤①②，沿虚线对折2次，然后沿图③的虚线剪去一个角，展开铺平后得到图④，若图③中
，
，则四边形
与原正方形纸面积比为（ ）
A.
B.
C.
D.
【答案】D
【解析】
设原正方形的边长为a，根据图3中
，
，得到图④中的图形中的线段关系，求出四边形
的面积，即可求解.
根据图示的方法折叠可知四边形为菱形，
∵图③中，，
故在图④中，可知G为OQ中点，∠OHG=30°，
设原正方形的面积为a，则PQ=a，S正方形MNQP=a2,
故OQ=
∴OG=
OQ=
，EG=2OG=
∵∠OHG=30°
∴HG=2OG=，OH=
=
∴HF=2OH=
∴S四边形EFGH=EG×HF=
a2,
∴四边形与原正方形纸面积比为a2：a2=，
故选D.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
