题目内容
锐角△ABC中，a=1，b=2，则c边的取值范围是________（用不等式表示）．
1＜c＜
分析：根据三角形三边关系：两边之和大于第三边，两边之差小于第三边，来确定c的取值范围．
解答：∵△ABC中，a=1，b=2，
∴2-1＜c＜1+2，
∴c的取值范围为：1＜c＜3．
当△ABC是以c为斜边的直角三角形时：c=
=．
则1＜c＜．
故答案为：1＜c＜．
点评：此题主要考查对三角形三边关系的理解及运用．
分析：根据三角形三边关系：两边之和大于第三边，两边之差小于第三边，来确定c的取值范围．
解答：∵△ABC中，a=1，b=2，
∴2-1＜c＜1+2，
∴c的取值范围为：1＜c＜3．
当△ABC是以c为斜边的直角三角形时：c=
=．则1＜c＜
．故答案为：1＜c＜
．点评：此题主要考查对三角形三边关系的理解及运用．
练习册系列答案
相关题目
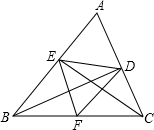在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①DF=EF；②AD：AB=AE：AC；③△DEF是等边三角形；④BE+CD=BC；⑤当∠ABC=45°时，BE=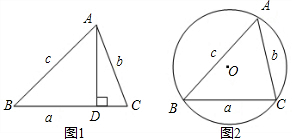
15、已知，如图，锐角△ABC中，AD⊥BC于D，H为垂心（三角形三条高线的交点）；在AD上有一点P，且∠BPC为直角．