题目内容
 如图,大正方形由四个完全相同的直角三角形和中间的小正方形构成,已知直角三角形较短的直角边为2,小正方形边长为a.
如图,大正方形由四个完全相同的直角三角形和中间的小正方形构成,已知直角三角形较短的直角边为2,小正方形边长为a.(1)请用含字母a的代数式表示大正方形的面积;
(2)当a=1时,这个大正方形的面积是多少?
分析:(1)由于直角三角形较短的直角边为2,小正方形边长为a,所以直角三角形较长的直角边为a+2,根据勾股定理求出直角三角形斜边的平方,即为大正方形的面积;
(2)将a=1代入(1)中所求的代数式,即可得到这个大正方形的面积.
(2)将a=1代入(1)中所求的代数式,即可得到这个大正方形的面积.
解答:解:(1)∵直角三角形较短的直角边为2,小正方形边长为a,
∴直角三角形较长的直角边为a+2,
∴大正方形的面积=直角三角形斜边的平方=(a+2)2+a2=2a2+4a+4;
(2)当a=1时,大正方形的面积=12+4×1+8=1+4+8=13.
∴直角三角形较长的直角边为a+2,
∴大正方形的面积=直角三角形斜边的平方=(a+2)2+a2=2a2+4a+4;
(2)当a=1时,大正方形的面积=12+4×1+8=1+4+8=13.
点评:本题考查了列代数式,勾股定理,代数式求值,解决问题的关键是仔细观察,发现直角三角形较长的直角边为a+2.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
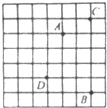 15、如图,大正方形是由49个边长为l的小正方形拼成的,A,B,C,D四个点是小正方形的顶点,由其中三个点为顶点的直角三角形的个数是( )
15、如图,大正方形是由49个边长为l的小正方形拼成的,A,B,C,D四个点是小正方形的顶点,由其中三个点为顶点的直角三角形的个数是( )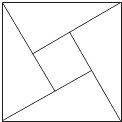 四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,每个直角三角形两直角边的和是5,则中间小正方形的面积等于
四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如图,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,每个直角三角形两直角边的和是5,则中间小正方形的面积等于
 如图,大正方形由四个完全相同的直角三角形和中间的小正方形构成,已知直角三角形较短的直角边为2,小正方形边长为a.
如图,大正方形由四个完全相同的直角三角形和中间的小正方形构成,已知直角三角形较短的直角边为2,小正方形边长为a.