题目内容
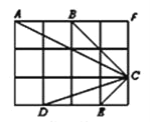
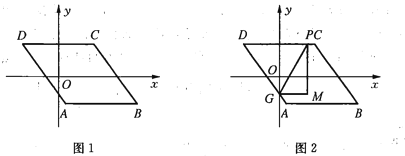
【题目】如图1,已知![]() ,
,![]() 轴,
轴,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第四象限.点
在第四象限.点![]() 是
是![]() 边上的一个动点.
边上的一个动点.
(1)若点![]() 在边
在边![]() 上,
上,![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若点![]() 在边
在边![]() 或
或![]() 上,点
上,点![]() 关于一条坐标轴对称的点
关于一条坐标轴对称的点![]() 落在直线
落在直线![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)若点![]() 在边
在边![]() 、
、![]() 或
或![]() 上,点
上,点![]() 是
是![]() 与
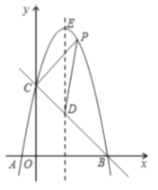
与![]() 轴的交点,如图2,过点
轴的交点,如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,它们相交于点
,它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标(直接写出答案).
的坐标(直接写出答案).
【答案】(1)点![]() 的坐标为
的坐标为![]() ;
;
(2)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;
(3)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或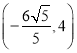 或
或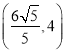 .
.
【解析】
(1)由题意点P与点C重合,可得点P坐标为(3,4);
(2)分两种情形①当点P在边AD上时,②当点P在边AB上时,分别列出方程即可解决问题;
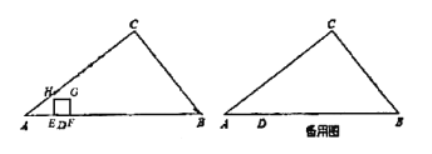
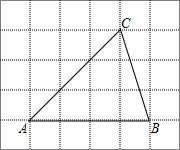
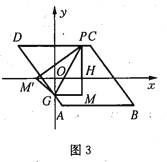
(3)分三种情形①如图2中,当点P在线段CD上时.②如图3中,当点P在AB上时.@如图4中,当点P在线段AD上时,分别求解即可;
解:(1)在![]() 中,
中,![]() ,
,
∴点![]() 与点
与点![]() 重合,
重合,
∴点![]() 的坐标为
的坐标为![]() .
.
(2)①当点![]() 在边
在边![]() 上时,由已知得,直线
上时,由已知得,直线![]() 的函数表达式为
的函数表达式为![]() ,
,
设![]() ,且
,且![]() ,
,
若点![]() 关于
关于![]() 轴对称点
轴对称点![]() 在直线
在直线![]() 上,
上,
则![]() ,
,
解得![]() ,
,
此时![]() .
.
若点![]() 关于
关于![]() 轴对称点
轴对称点![]() 在直线
在直线![]() 上,
上,
则![]() ,
,
解得![]() ,
,
此时![]() .
.
②当点![]() 在边
在边![]() 上时,设
上时,设![]() ,且
,且![]() ,
,
若点![]() 关于
关于![]() 轴对称点
轴对称点![]() 在直线
在直线![]() 上,
上,
则![]() ,
,
解得![]() ,
,
此时![]() .
.
若点![]() 关于
关于![]() 轴对称点
轴对称点![]() 在直线
在直线![]() 上,
上,
则![]() ,
,
解得![]() ,
,
此时![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
(3)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或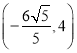 或
或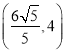 .
.
解答如下:
∵直线![]() 为
为![]() ,
,
∴![]() .
.
①如图3,当点![]() 在
在![]() 边上时,可设
边上时,可设![]() ,且
,且![]() ,则可得
,则可得![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,则
,则![]() ,即
,即![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,解得
,解得![]() 或
或![]() ,
,
即 或
或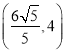 ;
;
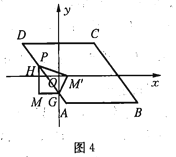
②如图4,当点![]() 在
在![]() 边上时,设
边上时,设![]() ,则
,则![]() ,
,![]() .同上可证得
.同上可证得![]() ,则
,则![]() ,即
,即![]() ,则
,则![]() ,在
,在![]() 中,由勾股定理得
中,由勾股定理得![]() ,解得
,解得![]() ,则
,则![]() ;
;
③如图5,当点![]() 在
在![]() 边上时,设
边上时,设![]() ,此时
,此时![]() 在
在![]() 轴上,则四边形
轴上,则四边形![]() 是正方形,所以
是正方形,所以![]() ,则
,则![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或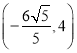 或
或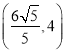 .
.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案【题目】甲、乙人5场10次投篮命中次数如图
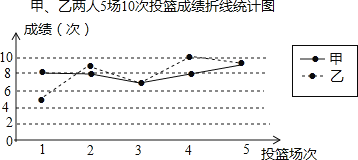
(1)填写表格.
平均数 | 众数 | 中位数 | 方差 | |
甲 | ______ | 8 | 8 | ______ |
乙 | 8 | ______ | ______ | 3.2 |
(2)①教练根据这5个成绩,选择甲参加投篮比赛,理由是什么?
②如果乙再投篮1场,命中8次,那么乙的投监成绩的方差将会怎样变化?(“变大”“变小”或”不变”)