题目内容
17.对于正整数n,记n!=1×2×3×…×(n-1)×n,例如:4!=24,5!=120,则2015!的尾部(从个位往前计数)连续的0的个数是425.分析 根据n!=1×2×3×…×(n-1)×n即可得出“5!的末尾有1个连续的0,10!的末尾有2个连续的0,100!的末尾有10×2+1=21个连续的0,1000!的末尾有=10×21+1=211个连续的0”,再根据2015由2个千、1个十和5个一组成,即可得出2015!的尾部(从个位往前计数)连续的0的个数.
解答 解:∵n!=1×2×3×…×(n-1)×n,且2×5=10,
∴5!的末尾有1个连续的0,10!的末尾有2个连续的0,100!的末尾有10×2+1=21个连续的0,1000!的末尾有=10×21+1=211个连续的0.
∵2015由2个千、1个十和5个一组成,
∴2015!的末尾有211×2+2×1+1=425个连续的0.
故答案为:425.
点评 本题考查了规律型中数字的变化类,根据新定义式n!=1×2×3×…×(n-1)×n找出“5!的末尾有1个连续的0,10!的末尾有2个连续的0,100!的末尾有10×2+1=21个连续的0,1000!的末尾有=10×21+1=211个连续的0.”是解题的关键.

练习册系列答案
相关题目
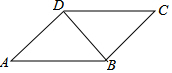 如图,已知?ABCD.
如图,已知?ABCD.