题目内容
若抛物线y=mx2+(m+2)x+
的顶点在坐标轴上,则m= .
| 9 |
| 4 |
考点:二次函数的性质
专题:
分析:由于抛物线的顶点在坐标轴上,故应分在x轴上与y轴上两种情况进行讨论.
解答:解:①当抛物线y=mx2+(m+2)x+
的顶点在x轴上时,△=0,m≠0,
△=(m+2)2-4×m×(m+2)=0,
整理,得2m2-5m+2=0,
解得m=-2或
;
②当抛物线y=mx2+(m+2)x+
的顶点在y轴上时,
x=-
=0,
解得m=-2.
故答案为:-2或
.
| 9 |
| 4 |
△=(m+2)2-4×m×(m+2)=0,
整理,得2m2-5m+2=0,
解得m=-2或
| 2 |
| 3 |
②当抛物线y=mx2+(m+2)x+
| 9 |
| 4 |
x=-
| m+2 |
| m |
解得m=-2.
故答案为:-2或
| 2 |
| 3 |
点评:本题考查的是二次函数的性质,解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目
小月同学在某搜索引擎中输入“钓鱼岛最新消息”,能搜到与之相关的结果个数约为4680000,这个数用科学记数法表示为( )
| A、4.68×107 |
| B、46.8×106 |
| C、0.468×107 |
| D、4.68×106 |
某商店卖出两件衣服,每件卖45元,其中一件赚25%,另一件赔了25%,那么这两件衣服售出后商店是( )
| A、赔了9元 | B、赚了9元 |
| C、不赚不赔 | D、赔了6元 |
如果x-2=0与1-
=0的解相同,那么k的值是( )
| x+k |
| 3 |
A、
| ||
| B、1 | ||
| C、3 | ||
| D、-3 |
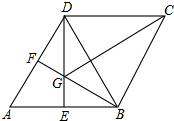 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接BD、CG.给出以下结论,其中正确的有( )
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接BD、CG.给出以下结论,其中正确的有( )①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ADE=
| ||
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列式子中:①3x-5;②2a-3=0;③7>-3;④5-7=-2;⑤|x|=1;⑥2x2+x=1.是等式的有( )
| A、6个 | B、5个 | C、4个 | D、3个 |