题目内容
 如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AB2的值为
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AB2的值为考点:全等三角形的判定与性质,勾股定理
专题:计算题
分析:由题意得到三角形AEG与三角形FGD相似,得到∠A=∠F,再由一对直角相等,BC=EC,利用AAS得到三角形ABC与三角形EFC全等,利用全等三角形对应边相等得到AB=FC,在直角三角形ECF中,利用勾股定理求出FC2的值,即为AB2的值.
解答: 解:∵EF⊥AC,CD⊥AB,
解:∵EF⊥AC,CD⊥AB,
∴∠AEF=∠ADF=90°,
∵∠AGE=∠FGD,
∴∠A=∠F,
在△ACD和△FCE中,
,
∴△ACD≌△FCE(AAS),
∴AB=FC,
在Rt△ECF中,EC=BC=2cm,EF=5cm,
根据勾股定理得:AB2=FC2=EF2+EC2=4+25=29.
故答案为:29
 解:∵EF⊥AC,CD⊥AB,
解:∵EF⊥AC,CD⊥AB,∴∠AEF=∠ADF=90°,
∵∠AGE=∠FGD,
∴∠A=∠F,
在△ACD和△FCE中,
|
∴△ACD≌△FCE(AAS),
∴AB=FC,
在Rt△ECF中,EC=BC=2cm,EF=5cm,
根据勾股定理得:AB2=FC2=EF2+EC2=4+25=29.
故答案为:29
点评:此题考查了全等三角形的判定与性质,以及勾股定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,△ABC中,DE∥BC,AD=5,BD=10,AE=3,则AC的值为
如图,△ABC中,DE∥BC,AD=5,BD=10,AE=3,则AC的值为 在平面直角坐标系中,点A、B的坐标分别为A(4,0),B(0,-4),BD是△ABO的角平分线,过O作OT⊥BD于T点,求
在平面直角坐标系中,点A、B的坐标分别为A(4,0),B(0,-4),BD是△ABO的角平分线,过O作OT⊥BD于T点,求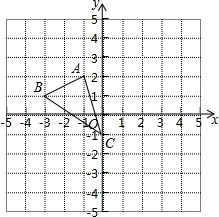 如图所示,已知△ABC.
如图所示,已知△ABC.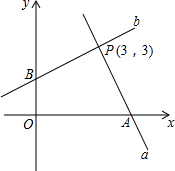 如图,相交于P(3,3)的互相垂直的两直线a、b中直线a与x轴正半轴交于点A,直线b与y轴正半轴交于点B.
如图,相交于P(3,3)的互相垂直的两直线a、b中直线a与x轴正半轴交于点A,直线b与y轴正半轴交于点B.