题目内容
若直角三角形的两条直角边长为a、b，且满足
+|b-4|=0，则该直角三角形的斜边长为 ．
| a-3 |
考点：勾股定理,非负数的性质：绝对值,非负数的性质：算术平方根
专题：
分析：先根据非负数的性质求出a、b的值，再根据勾股定理求出斜边的长即可．
解答：解：∵
+|b-4|=0，
∴a-3=0，b-4=0，解得a=3，b=4，
∴该直角三角形的斜边长=
=
=5．
故答案为：5．
| a-3 |
∴a-3=0，b-4=0，解得a=3，b=4，
∴该直角三角形的斜边长=
| a2+b2 |
| 32+42 |
故答案为：5．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
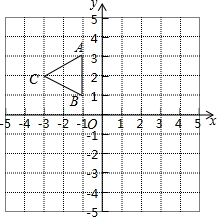如图，△ABC三个顶点坐标分别为A（-1，3），B（-1，1），C（-3，2），以原点O为位似中心，将△ABC放大为原来的2倍得到△A1B1C1，请在第四象限内画出△A1B1C1，并写出A1、B1、C1三点的坐标．
如图，Rt△ADB中，∠D=90°，∠A=32°，C为边AD上一点，C与点A、D不重合，设∠ACB的度数为x，则x的取值范围是已知实数x、y满足2
+3（y+1）2=0，则x-y=（ ）
| x-2 |
| A、3 | B、-3 | C、1 | D、-1 |