题目内容
证明命题“等腰三角形底边上的中点到两腰的中点距离相等”。
已知:在△ABC中,_____________________________
求证:____________________
证明:
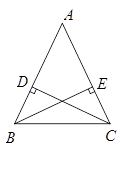
已知:在△ABC中,AB=AC,且D、E、F分别是BC、AB、AC的中点;
求证:DE="DF"
证明:证明:∵△ABC为等腰三角形,
∴∠B=∠C,AB=AC.
又点D,E,F分别为边BC,AB,AC的中点,
∴BE=CF,BD=CD.
∴△BDE≌△CDF.
∴DE=DF.
故命题得证.
解析试题分析:根据命题,画出图形,写出已知及求证的内容,并利用等腰三角形的性质证明.
由命题可知:在△ABC中,AB=AC,点D,E,F分别为边BC,AB,AC的中点;
求证:DE=DF;
证明:∵△ABC为等腰三角形,
∴∠B=∠C,AB=AC.
又点D,E,F分别为边BC,AB,AC的中点,
∴BE=CF,BD=CD.
∴△BDE≌△CDF.
∴DE=DF.
故命题得证.
考点:等腰三角形的性质,全等三角形的判定和性质
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考的热点,一般难度不大,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 证明命题“等腰三角形两腰上的高线相等”.
证明命题“等腰三角形两腰上的高线相等”.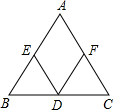 证明命题“等腰三角形底边上的中点到两腰的中点距离相等”.
证明命题“等腰三角形底边上的中点到两腰的中点距离相等”.