题目内容
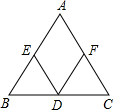证明命题“等腰三角形底边上的中点到两腰的中点距离相等”．已知：在△ABC中，
AB=AC，点D，E，F分别为边BC，AB，AC的中点．
AB=AC，点D，E，F分别为边BC，AB，AC的中点．
求证：
DE=DF
DE=DF
证明：
分析：证明命题时，首先根据题意画出图形，再结合图形写出已知及求证的内容，然后利用已学知识进行证明．
解答：已知：在△ABC中，AB=AC，点D，E，F分别为边BC，AB，AC的中点．
求证：DE=DF．
证明：∵△ABC为等腰三角形，
∴∠B=∠C，AB=AC．
又∵点D，E，F分别为边BC，AB，AC的中点，
∴BE=CF，BD=CD，
∴△BDE≌△CDF．
∴DE=DF．
故命题得证．
求证：DE=DF．
证明：∵△ABC为等腰三角形，
∴∠B=∠C，AB=AC．
又∵点D，E，F分别为边BC，AB，AC的中点，
∴BE=CF，BD=CD，
∴△BDE≌△CDF．
∴DE=DF．
故命题得证．
点评：本题主要考查命题的证明步骤，等腰三角形的性质及全等三角形的性质与判定．根据命题画出图形是解题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
证明命题“等腰三角形两腰上的高线相等”．