题目内容
 如图,已知直线y=-
如图,已知直线y=-| 1 |
| 2 |
考点:相似三角形的判定,一次函数图象上点的坐标特征
专题:
分析:先求出AB两点的坐标,再根据△AOB∽△COB,△AOB∽△BOC两种情况进行讨论.
解答:解:∵直线y=-
x+2与x轴交于点A,与y轴交于点B,
∴A(4,0),B(0,2).
当△AOB∽△COB时,
=
=1,即
=1,
∴OC=4,
∴C(-4,0),(4,0);
当△AOB∽△BOC时,
=
,即
=
,解得OC=1,
∴C(-1,0),(1,0).
综上所述,C(-4,0)或(4,0)或(-1,0)或(1,0).
故答案为:(-4,0)或(4,0)或(-1,0)或(1,0).
| 1 |
| 2 |
∴A(4,0),B(0,2).
当△AOB∽△COB时,
| OA |
| OC |
| OB |
| OB |
| 4 |
| OC |
∴OC=4,
∴C(-4,0),(4,0);
当△AOB∽△BOC时,
| OA |
| OB |
| OB |
| OC |
| 4 |
| 2 |
| 2 |
| OC |
∴C(-1,0),(1,0).
综上所述,C(-4,0)或(4,0)或(-1,0)或(1,0).
故答案为:(-4,0)或(4,0)或(-1,0)或(1,0).
点评:本题考查的是相似三角形的判定,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
下列变形不正确的是( )
| A、4x-5=3x+2变形得4x-3x=2+5 | ||||
B、3x=2变形得x=
| ||||
C、
| ||||
D、
|
下列各组数是勾股数的为( )
| A、32,42,52 |
| B、4,5,6 |
| C、8,15,19 |
| D、7,24,25 |
 如图,△ABC中,AC=AB,以AB为直径作⊙O,交BC于D,交AC于E,试说明∠BAD和∠EDC之间的数量关系.
如图,△ABC中,AC=AB,以AB为直径作⊙O,交BC于D,交AC于E,试说明∠BAD和∠EDC之间的数量关系.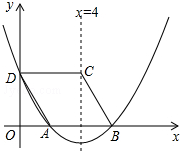 如图,抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点D(0,3),其对称轴为直线x=4,点C为对称轴上一点,四边形ABCD为平行四边形.
如图,抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点D(0,3),其对称轴为直线x=4,点C为对称轴上一点,四边形ABCD为平行四边形. 小明家有一块如图所示的地,其中阴影部分是两个正方形,其他的是两个直角三角形和一个正方形,大直角三角形的斜边和一条直角边的长分别为34米,30米,小明家打算在阴影部分的土地上种花生,则种花生的面积为
小明家有一块如图所示的地,其中阴影部分是两个正方形,其他的是两个直角三角形和一个正方形,大直角三角形的斜边和一条直角边的长分别为34米,30米,小明家打算在阴影部分的土地上种花生,则种花生的面积为