题目内容
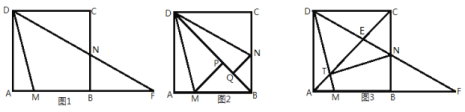
【题目】如图，在正方形ABCD中，点M、N分别在AB、BC边上，∠MDN=45°．
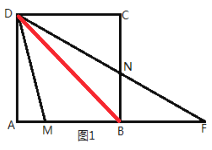
（1）如图1，DN交AB的延长线于点F． 求证：
；
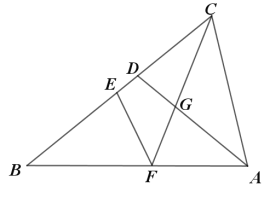
（2）如图2，过点M作MP⊥DB于P，过N作NQ⊥BD于
，若
，求对角线BD的长；
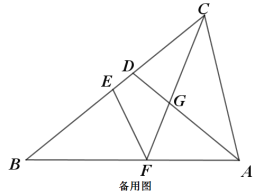
（3）如图3，若对角线AC交DM，DF分别于点T，E．判断△DTN的形状并说明理由．
【答案】（1）证明见解析；（2）
；（3）
是等腰直角三角形，理由见解析
【解析】
（1）连接BD，根据正方形的性质可证出
，得到
，即可得到结果；
（2）根据正方形ABCD，可得到
，
，可推出
，得到
，于是推出
，得到
，进而得出
，代入已知条件即可；
（3）由已知条件证出
，可得
，再根据
，得到
，所以
，代入条件可求得结果．
解：（1）连接BD
∵四边形ABCD是正方形
∴
∴
又∵
∴
又∵
∴
∴
∴
（2）∵正方形ABCD
∴，
又∵
∴
又∵
，
∴
∴
∴
∴
∴
又∵
∴
∴
故答案为：
（3）是等腰直角三角形，理由如下：
由
，
，
∴
又∵
∴
∴
又∵
∴
∴是等腰直角三角形
练习册系列答案
相关题目
