题目内容
8.为了进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙两种树的价格相同,丙种树每棵的价格是甲、乙的1.5倍,甲种树每棵200元,现计划用210000元,购买这三种树共1000棵,(1)若购买甲种树的棵树是乙种树的2倍,且恰好用完计划资金,求三种树各购买多少棵?
(3)若又增加了10120元的购树款,在购买总棵树不变的情况下,求丙种树最多可以购买多少棵?
分析 (1)利用已知甲种树每棵200元,即可求出乙、丙两种树每棵钱数,设购买乙种树x棵,则购买甲种树2x棵,丙种树(1000-3x)棵,根据现计划用210000元资金购买这三种树共1000棵,得出等式方程,求出即可;
(2)假设购买丙种树y棵,则甲、乙两种树共(1000-y)棵,根据题意得:200(1000-y)+300y≤210000+10120,求出即可.
解答 解:(1)∵甲种树每棵200元,
∴乙种树每棵200元,丙种树每棵树300元,
设购买乙种树x棵,则购买甲种树2x棵,丙种树(1000-3x)棵.
根据题意:200×2x+200x+300(1000-3x)=210000,
解得:x=300
则2x=600,1000-3x=100,
答:能购买甲种树600棵,乙种树300棵,丙种树100棵;
(2)设购买丙种树y棵,则甲、乙两种树共(1000-y)棵,
根据题意得:200(1000-y)+300y≤210000+10120,
解得:y≤201.2,
∵y为正整数,
∴y最大取201.
答:丙种树最多可以购买201棵.
点评 本题考查一元一次不等式的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.本题难点是(2)中总钱数变化,购买总棵树不变的情况下得出不等式方程.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.下列运算正确的是( )
| A. | 3x-2x=1 | B. | -2x-2=-$\frac{1}{2{x}^{2}}$ | C. | (-a)2•a3=a6 | D. | (-a2)3=-a6 |
3.不等式x>-1在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
17.已知一副三角板如图(1)放置,其中两条斜边互相平行,则图(2)中∠1为( )

| A. | 25° | B. | 30° | C. | 15° | D. | 20° |
18.-$\frac{1}{2015}$的相反数是( )
| A. | 2 015 | B. | -2 015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
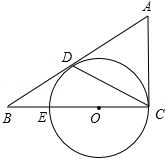 如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.