题目内容
15.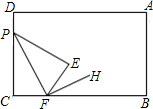 如图,将长方形纸片ABCD的角C沿PF折叠,使点C落在长方形的内部点E处,若FH平分∠BFE,则∠PFH的度数( )
如图,将长方形纸片ABCD的角C沿PF折叠,使点C落在长方形的内部点E处,若FH平分∠BFE,则∠PFH的度数( )| A. | 90°<a<180° | B. | 0°<a<90° | ||
| C. | a=90° | D. | a随折痕FH位置的变化而变化 |
分析 首先根据折叠方法可得∠1=∠3=$\frac{1}{2}$∠CFE,再根据角平分线性质可知:∠2=∠4,由图形可知∠1+∠2+∠3+∠4=180°,故∠1+∠2=90°,进而得到∠PFH的度数.
解答 解:如图,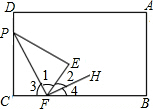
∵△PFE是由△PFC沿PF折叠,
∴∠1=∠3=$\frac{1}{2}$∠CFE,
∵FH平分∠BFE,
∴∠2=∠4=$\frac{1}{2}$∠EFB,
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠2=90°,
即:∠PFH=90°.
故选C.
点评 此题主要考查了翻折变换以及角平分线的性质,解决问题的关键是根据翻折的方法得到∠1和∠3的关系,根据角平分线的性质得到∠2和∠4的关系.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | 2x2•x3=2x5 | B. | (x-2)2=x2-4 | C. | x2+x3=x5 | D. | (x3)4=x7 |
6.下列式子不是二次根式的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{a}$(a≥0) | C. | $\sqrt{{a^2}+1}$ | D. | $\sqrt{-2}$ |
10.对于代数式3x3y-2x2y2+5xy3-1,下列说法不正确的是( )
| A. | 它按y的升幂排列 | B. | 它按x的降幂排列 | C. | 它的常数项是-1 | D. | 它是四次四项式 |
 沿虚线剪去长方形纸片相邻的两个角,使∠1=115°,则∠2=155°.
沿虚线剪去长方形纸片相邻的两个角,使∠1=115°,则∠2=155°.