题目内容
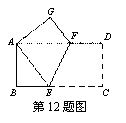
如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F. 点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.
(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值. 进而猜想:对于任意一点P,PD与PF的差为定值. 请你判断该猜想是否正确,并说明理由;
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.
请直接写出所有“好点”的个数,并求出△PDE的周长最小时“好点”的坐标.
 |  | ||
(1) ;(2)设P(a,
;(2)设P(a, ),则F(a, 8),∵ D(0,6) ∴ PD=
),则F(a, 8),∵ D(0,6) ∴ PD= , ∴ PD-PF=2,
, ∴ PD-PF=2,
(3)P(a,  ),
), , ∴ S△=
, ∴ S△=
 ,
,
 , ∵ -8≤a≤0 ∴ 4≤S△≤13,
, ∵ -8≤a≤0 ∴ 4≤S△≤13,
∴ 三角形面积可以等于4到13所有整数,在面积为12时a的值有两个,所以面积为整数时好点有11个,经过验证周长最小时的好点包含这11个之内,所以好点共11个;周长最小即PD+PE最小即可, ∵ PD=PF+2,
∴ PF+PE之和最小即可,所以此时P、E、F三点共线,此时P(-4,6),
综上,11个好点,P(-4,6).

练习册系列答案
相关题目
在某校初三年级古诗词比赛中,初三(1)班42名学生的成绩统计如下:
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 1 | 2 | 8 | 13 | 14 | 4 |
则该班学生成绩的中位数和众数分别是( )
A.70,80 B.70,90 C.80,90 D.80,100


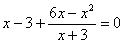 .
. 交于点A(1,a),则k= .
交于点A(1,a),则k= .


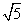 D.AF=EF
D.AF=EF