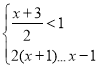题目内容
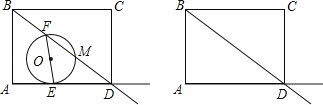
【题目】已知一副直角三角板如图放置，其中BC＝6，EF＝8，把30°的三角板向右平移，使顶点B落在45°的三角板的斜边DF上，则两个三角板重叠部分（阴影部分）的面积为_____．
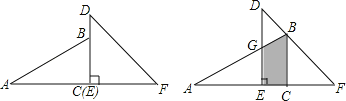
【答案】12﹣
【解析】
根据等腰直角三角形的性质可得CF＝BC＝6，然后求出EC的长，再根据锐角三角函数即可求出AC的长，再利用锐角三角函数求出EG的长，最后根据梯形的面积公式计算即可．
解：在直角△BCF中，
∵∠F＝45°，BC＝6，
∴CF＝BC＝6．
又∵EF＝8，
则EC＝2．
在直角△ABC中，
∵BC＝6，∠A＝30°，
∴AC＝
＝6
，
则AE＝6﹣2，∠A＝30°，
∴EG＝AE·tanA＝6﹣，
阴影部分的面积为：
（EG+BC）EC＝×（6﹣+6）×2＝12﹣．
故答案是：12﹣．
练习册系列答案
阅读快车系列答案
相关题目
