题目内容
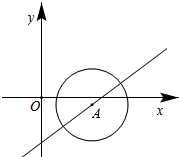 如图,半径为1.2的⊙A,圆心在直线y=
如图,半径为1.2的⊙A,圆心在直线y=| 3 |
| 4 |
考点:切线的性质,一次函数图象上点的坐标特征
专题:
分析:连接AP,在Rt△AOP中,AO=1.2,则当OA最小时OP有最小值,所以当OA与直线垂直时OP最小,设直线与x轴、y轴的交点分别为B、C,利用等积法可求得O到直线的距离,再结合勾股定理可求得OP的值.
解答: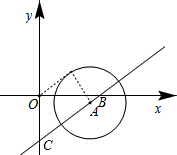 解:如图,连接AP,则AP⊥OP,设直线y=
解:如图,连接AP,则AP⊥OP,设直线y=
x-3与x轴、y轴分别交与点B、C,
在Rt△OAP中,AP=1.2,由勾股定理可得OP=
=
,
∴当OA最小时,OP最小,
∴当OA⊥BC时,OP最小,
在y=
x-3中,令y=0解得x=4,令x=0解得y=-3,
∴OB=4,OC=3,由勾股定理可知BC=5
在Rt△OBC中,由面积相等可知OA•BC=OB•OC,
即5OA=12,解得OA=2.4,
此时OP=
=
,
综上可知,OP的最小值为
.
故答案为:
.
 解:如图,连接AP,则AP⊥OP,设直线y=
解:如图,连接AP,则AP⊥OP,设直线y=| 3 |
| 4 |
在Rt△OAP中,AP=1.2,由勾股定理可得OP=
| OA2-PA2 |
| OA2-1.44 |
∴当OA最小时,OP最小,
∴当OA⊥BC时,OP最小,
在y=
| 3 |
| 4 |
∴OB=4,OC=3,由勾股定理可知BC=5
在Rt△OBC中,由面积相等可知OA•BC=OB•OC,
即5OA=12,解得OA=2.4,
此时OP=
| 2.42-1.22 |
6
| ||
| 5 |
综上可知,OP的最小值为
6
| ||
| 5 |
故答案为:
6
| ||
| 5 |
点评:本题主要考查切线的性质及勾股定理,根据条件求出OP最小时P点的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若某人沿坡角为α的斜坡前进100m,则他上升的最大高度是( )
| A、100sinα m | ||
B、
| ||
C、
| ||
| D、100cosα m |
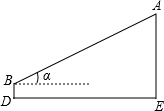 如图,为测量树AE的高,在和E相距a m的D处放测倾器BD,测得树顶A的仰角为α,测倾器高BD=h m,则树高AE为
如图,为测量树AE的高,在和E相距a m的D处放测倾器BD,测得树顶A的仰角为α,测倾器高BD=h m,则树高AE为