题目内容
若1+2+3+4+…+100=a,则100+101+102+103+…+199用含a的代数式表示为( )
A.100a B.100+a C.9900+a D.10000+a
C 【解析】 【解析】 100+101+102+103+…+199=100+100+1+100+2+100+3+100+4+…+100+99 =100×100+(1+21+3+4+…+98+99)=100×99+(1+2+3+…+98+99+100) =9900+a, 故选:C.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
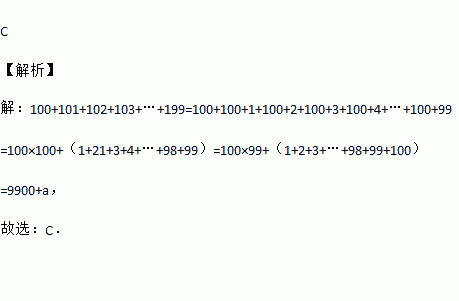


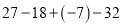 ; (2)
; (2)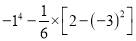 .
.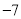 C.
C. 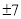 D. 0和7
D. 0和7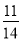 B.
B. 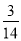 C.
C. 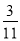 D.
D. 