题目内容
10.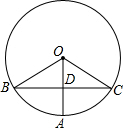 如图,⊙O的半径OA=3,OA的垂直平分线交⊙O于B、C两点,连接OB、OC,用扇形OBC围成一个圆锥的侧面,则这个圆锥的高为2$\sqrt{2}$.
如图,⊙O的半径OA=3,OA的垂直平分线交⊙O于B、C两点,连接OB、OC,用扇形OBC围成一个圆锥的侧面,则这个圆锥的高为2$\sqrt{2}$.
分析 求出△OAB和△AOC都是等边三角形,求出∠BOC=120°,根据弧长公式求出圆锥的半径,根据勾股定理求出即可.
解答 解:连接AB,AC,
∵BC为OA的垂直平分线,
∴OB=AB,OC=AC,
∴OB=AB=OA,OC=OA=AC,
∴△OAB和△AOC都是等边三角形,
∴∠BOA=∠AOC=60°,
∴∠BOC=120°,
设圆锥的底面半径为r,则2πr=$\frac{120π×3}{180}$,
解得:r=1,
这个圆锥的高为$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查了等边三角形的性质和判定,勾股定理,弧长公式等知识点,能求出圆锥的半径是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.2016年,广东省实现国民生产总值(GDP)约79500亿元,已连续28年位居全国第一,将79500亿元用科学记数法表示应为( )
| A. | 7.95×1012元 | B. | 79.5×1011元 | C. | 7.95×1011元 | D. | 7.95×1013元 |
5.样本数据3,2,4,a,8的平均数是4,则这组数据的众数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
2.下列实数中,有理数是( )
| A. | $\root{3}{4}$ | B. | $\frac{π}{2}$ | C. | $\sqrt{8}$ | D. | 3.14159 |
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)