题目内容
在△ABC中,∠ABC=90°,BC=AB,P是内一点,且PA=1,PB=2,PC=3,试求∠APB的度数.
考点:旋转的性质,勾股定理的逆定理,等腰直角三角形
专题:
分析:由于∠ABC=90°,BC=AB,则可以把△PBC绕B点逆时针旋转90°得到△DBA,根据旋转的性质得到BD=BP=2,AD=PC=3,∠PBD=90°,得到△PBD为等腰直角三角形,根据等腰直角三角形的性质得到PD=
PB=2
,∠DPB=45°,在△APD中易得AP2+PD2=AD2,根据勾股定理的逆定理得到△APD为直角三角形,然后利用∠APB=∠APD+∠DPB计算即可.
| 2 |
| 2 |
解答:解: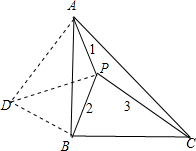 ∵∠ABC=90°,BC=AB,
∵∠ABC=90°,BC=AB,
∴把△PBC绕B点逆时针旋转90°得到△DBA,如图,
∴BD=BP=2,AD=PC=3,∠PBD=90°,
∴△PBD为等腰直角三角形,
∴PD=
PB=2
,∠DPB=45°,
在△APD中,AP=1,PD=2
,AD=3,
∵12+(2
)2=32,
∴AP2+PD2=AD2,
∴△APD为直角三角形,
∴∠APD=90°,
∴∠APB=∠APD+∠DPB=90°+45°=135°.
 ∵∠ABC=90°,BC=AB,
∵∠ABC=90°,BC=AB,∴把△PBC绕B点逆时针旋转90°得到△DBA,如图,
∴BD=BP=2,AD=PC=3,∠PBD=90°,
∴△PBD为等腰直角三角形,
∴PD=
| 2 |
| 2 |
在△APD中,AP=1,PD=2
| 2 |
∵12+(2
| 2 |
∴AP2+PD2=AD2,
∴△APD为直角三角形,
∴∠APD=90°,
∴∠APB=∠APD+∠DPB=90°+45°=135°.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等腰直角三角形的性质以及勾股定理的逆定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系中,将△ABC绕A点逆时针旋转90°后,B点对应点的坐标为( )
如图,在平面直角坐标系中,将△ABC绕A点逆时针旋转90°后,B点对应点的坐标为( )| A、(1,3) |
| B、(0,3) |
| C、(1,2) |
| D、(0,2) |
 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=| 5 |
| 6 |
| A、3,2 | ||
| B、2,1 | ||
C、
| ||
D、1,
|
 如图,△ABC为等边三角形,BD=DE,∠BDE=120°,连接CE,F为CE的中点,连接DF并倍长,连接AD、CG、AG.下列结论:
如图,△ABC为等边三角形,BD=DE,∠BDE=120°,连接CE,F为CE的中点,连接DF并倍长,连接AD、CG、AG.下列结论:①CG=DE;②若DE∥BC,则△ABH∽△GBD;③在②的条件下,若CE⊥BC,则
| AD |
| BD |
| ||
| 2 |
其中正确的有( )
| A、①②③都正确 |
| B、只有①②正确 |
| C、只有②③正确 |
| D、只有①③正确 |
已知2≤|x|≤3,则函数y=(x-1)2的取值范围是( )
| A、1≤y≤4和9≤y≤16 |
| B、9≤y≤16 |
| C、4≤y≤9 |
| D、1≤y≤9 |
已知
+|b-1|=0,那么a-b的值为( )
| a+2 |
| A、-3 | B、-1 | C、1 | D、3 |
 作图题:在∠AOB内有两点M、N,求作一点P使得PM=PN,且P到∠AOB两边的距离相等.要求尺规作图,不写作法,保留作图痕迹.
作图题:在∠AOB内有两点M、N,求作一点P使得PM=PN,且P到∠AOB两边的距离相等.要求尺规作图,不写作法,保留作图痕迹. 如图,二次函数y=ax2+bx的顶点为A(1,1),与x轴的一个交点为B,双曲线y=
如图,二次函数y=ax2+bx的顶点为A(1,1),与x轴的一个交点为B,双曲线y=