题目内容
 如图,△ABC的周长为L,面积为S,△ABC的三边中点组成△A1B1C1,△A1B1C1的三边中点组成△A2B2C2,如此进行下去,得到△AnBnCn,则△AnBnCn的周长为
如图,△ABC的周长为L,面积为S,△ABC的三边中点组成△A1B1C1,△A1B1C1的三边中点组成△A2B2C2,如此进行下去,得到△AnBnCn,则△AnBnCn的周长为考点:三角形中位线定理
专题:规律型
分析:根据三角形中位线定理可求得三边的长,从而不难求得△A1B1C1的周长,同理可求得另一三角形的周长,以此类推,从而可以发现规律;由于A1、B1、C1分别是△ABC的边BC、CA、AB的中点,就可以得出△A1B1C1∽△ABC,且相似比为
,就可求出S△A1B1C1=
,同样地方法得出S△A2B2C2=
,S△A3B3C3=
…所以就可以求出S△AnBnCn的值.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 64 |
解答:解:如图所示:
∵A1B1,B1C1,A1C1是△ABC的三条中位线,
∴A1B1=
AB,A1C1=
AC,C1B1=
CB,
∴△A1B1C1的周长=
(AB+AC+CB)=
L.
同理:A2B2C2的周长为
L,△A3B3C3的周长为
L,
∴△AnBnCn的周长为
L;
∵A1、B1、C1分别是△ABC的边BC、CA、AB的中点,
∴A1B1、A1C1、B1C1是△ABC的中位线,
∴△A1B1C1∽△ABC,且相似比为
∴S△A1B1C1:S△ABC=1:4,且S△ABC=S
∴S△A1B1C1=
S.
∵A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,
∴△A1B1C1的∽△A2B2C2且相似比为
∴S△A2B2C2=
S.依此类推
∴S△A3B3C3=
…
∴S△AnBnCn=
.
故答案为:
L,
S.

∵A1B1,B1C1,A1C1是△ABC的三条中位线,
∴A1B1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△A1B1C1的周长=
| 1 |
| 2 |
| 1 |
| 2 |
同理:A2B2C2的周长为
| 1 |
| 4 |
| 1 |
| 8 |
∴△AnBnCn的周长为
| 1 |
| 2n |
∵A1、B1、C1分别是△ABC的边BC、CA、AB的中点,
∴A1B1、A1C1、B1C1是△ABC的中位线,
∴△A1B1C1∽△ABC,且相似比为
| 1 |
| 2 |
∴S△A1B1C1:S△ABC=1:4,且S△ABC=S
∴S△A1B1C1=
| 1 |
| 4 |
∵A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,
∴△A1B1C1的∽△A2B2C2且相似比为
| 1 |
| 2 |
∴S△A2B2C2=
| 1 |
| 16 |
∴S△A3B3C3=
| 1 |
| 64 |
∴S△AnBnCn=
| 1 |
| 22n |
故答案为:
| 1 |
| 2n |
| 1 |
| 22n |
点评:本题考查了三角形的中位线定理以及相似三角形的判定和性质,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
计算
-
的结果是( )
| x2 |
| x-1 |
| 1 |
| x-1 |
| A、x2-1 |
| B、x-1 |
| C、x+1 |
| D、1 |
据相关媒体报道,2015年国家有望将房屋不动产纳入税务抵扣范围,此项改革或伴随房地产、建筑业“营改增”同步进行.分析称此项改革或带来超过8000亿元的减税规模,可进一步鼓励和刺激投资,房地产价格也可能因此调整.请用科学记数法表示出此项改革或带来超过多少元的减税规模( )
| A、8.0×1011 |
| B、8.0×1010 |
| C、8.0×106 |
| D、8.0×103 |
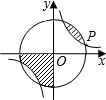 如图,已知点P(3a,a)是反比例函数y=
如图,已知点P(3a,a)是反比例函数y= 如图,直线l1:y=k1x+b与直线l2:y=k2x交于点(-1,3),则关于x的不等式k2x>k1x+b的解集为
如图,直线l1:y=k1x+b与直线l2:y=k2x交于点(-1,3),则关于x的不等式k2x>k1x+b的解集为 解不等式组,并把解集在所给的数轴上表示出来.
解不等式组,并把解集在所给的数轴上表示出来.