题目内容
已知正三角形的边长为6，则它的外接圆的面积为 ．
12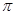
解析试题分析：设正△ABC的中心为O，过点O作OD⊥BC，垂足为D，连接OB，先根据正三角形的性质求得BD的长，∠OBD的度数，解直角三角形OBD即可求得外接圆的半径，从而求得外接圆的面积.
过点O作OD⊥BC，垂足为D，连接OB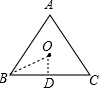
∵△ABC是等边三角形，
∴
，∠OBD=30°，
∴
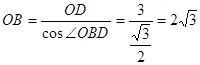
∴它的外接圆的面积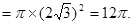
考点：正多边形和圆，解直角三角形
点评：解答本题的关键是正确画出正三角形及其中心，表示出正三角形外接圆的半径，把问题转化到直角三角形中求解.
练习册系列答案
相关题目
已知正三角形的边长为6，则其内切圆的半径为（ ）
A、2
| ||
| B、3 | ||
C、
| ||
| D、1 |
已知正三角形的边长为6，则这个正三角形的外接圆半径是（ ）
A、
| ||
B、2
| ||
| C、3 | ||
D、3
|
已知正三角形的边长为3，则它的外接圆的面积为（ ）
| A、3π | ||||
| B、6π | ||||
| C、9π | ||||
D、
|
如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于（ ）