Question

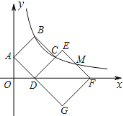
【题目】如图，正方形和正方形的顶点在轴上，顶点，在轴上，点在边上，反比例函数的图象经过点、和边的中点．若，则正方形的面积为（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

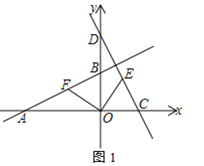
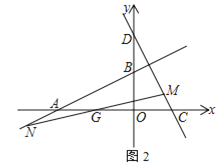
作BH⊥y轴于H，连结EG交x轴于N，如图，利用正方形DEFG的顶点D、F在x轴上，点C在DE边上，则∠EDF＝45°，于是可判断△AOD和△ABH都是等腰直角三角形，再根据正方形面积公式得到AB＝AD，所以OD＝OA＝AH＝BH1，则B点坐标为（1，2），接着根据反比例函数图象上点的坐标特征求出k得到反比例函数解析式为y，设DN＝a，则EN＝NF＝a，根据正方形的性质易得E（a+1，a），F（2a+1，0），然后利用线段中点坐标公式得到M点的坐标为（），再根据反比例函数图象上点的坐标特征2，接着解方程求出a的值，最后计算正方形DEFG的面积．

作BH⊥y轴于H，连结EG交x轴于N，如图，∵正方形ABCD和正方形DEFG的顶点A在y轴上，顶点D、F在x轴上，点C在DE边上，∴∠EDF＝45°，∴∠ADO＝45°，∴∠DAO＝∠BAH＝45°，∴△AOD和△ABH都是等腰直角三角形．

∵S正方形ABCD＝2，∴AB＝AD，∴OD＝OA＝AH＝BH1，∴B点坐标为（1，2），把B（1，2）代入y得：k＝1×2＝2，∴反比例函数解析式为y，设DN＝a，则EN＝NF＝a，∴E（a+1，a），F（2a+1，0）．

∵M点为EF的中点，∴M点的坐标为（）．

∵点M在反比例函数y的图象上，∴2，整理得：3a2+2a﹣8＝0，解得：a1，a2＝﹣2（舍去），∴正方形DEFG的面积＝2ENDF＝2．

故选B．