题目内容
13、用三种边长相等的正多边形铺地面，已选了正方形和正五边形两种，还应选正
二十
边形．分析：正多边形的组合能否铺满地面，关键是看位于同一顶点处的几个角之和能否为360°．因此用360°-正方形和正五边形内角度数和，即可求出应选的正多边形的内角度数，从而得出应选的正多边形．
解答：解：∵正方形和正五边形内角分别为90°、108°，
又∵360°-90°-108°=162°，
∴还应选正二十边形．
故答案为：二十．
又∵360°-90°-108°=162°，
∴还应选正二十边形．
故答案为：二十．
点评：本题考查了平面镶嵌（密铺）．几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．解决此类题，可以记住几个常用正多边形的内角．
练习册系列答案
相关题目
+
+
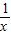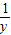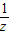的值为（ ）
